Anthony Watts has kindly offered the Talkshop the exclusive on Ned Nikolov and Karl Zeller’s reply to the article by Willis Eschenbach published at WUWT, which we accept, gladly.
Reply to: ‘The Mystery of Equation 8’ by Willis Eschenbach
Ned Nikolov, Ph.D. and Karl Zeller, Ph.D.
February 07,2012
In a recent article entitled ‘The Mystery of Equation 8’ published at WUWT on January 23 2012, Mr. Willis Eschenbach claims to have uncovered serious mathematical and conceptual flaws with two principal equations in our paper ‘Unified Theory of Climate‘. In his ‘analysis’, Mr. Eschenbach makes several fundamental errors, the nature of which were so elementary that our initial reaction was to not respond. However, after 10 days of observing the online discussion, it became clear that a number of bloggers have fallen victim to the same confusion as Mr. Eschenbach. Hence, we decided to prepare this official reply in an effort to set the record straight. This will be the only time that we respond to such confused criticism, since we believe that the climate science community has much more serious issues to discuss.
Demystifying the Mysteries of Equations 7 and 8
We begin with the most amusing claim by Mr. Eschenbach, which he calls ‘the sting in the tale’. First, some background: in our original paper, we use 3 principal equations that form the backbone of our new ‘Greenhouse’ concept. For consistency, we use here the same formula numbering as adopted in the original paper. Equation (2) calculates the mean surface temperature (Tgb) of a standard Planetary Gray Body (PGB) with no atmosphere, i.e.
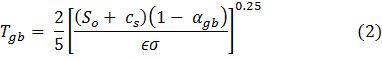where So is the solar irradiance (W m-2), αgb = 0.12 is the PGB shortwave albedo, ϵ = 0.955 is PGB’s thermal emissivity, σ = 5.6704×10-8 W m-2 K-4 is the SB constant, and cs = 0.0001325 W m-2 is a small constant, the purpose of which is to ensure that Tgb = 2.725K when So = 0.0. The derivation and validation of this formula is discussed in more detail elsewhere. We redefine the ‘Greenhouse Effect’ as a near-surface Atmospheric Thermal Enhancement (ATE) measured by the non-dimensional ratio (NTE) of a planet’s actual mean near-surface temperature (Ts) to the temperature of an equivalent PGB at the same distance from the Sun, i.e. NTE = Ts / Tgb(where Tgb is computed by Eq. 2). We then use observed data on surface temperature and atmospheric pressure (Ps) for 8 celestial bodies to derive an empirical function relating NTE to Ps employing non-linear regression analysis. The result is our Eq. (7), which describes all planetary data points with a high degree of accuracy:
The key conceptual implication of Eq. (7) is that, across a broad range of atmospheric planetary conditions, the ATE factor is completely explained by variations in mean surface pressure. In Section 3.3 of our original paper, we specifically point out that NTE has no meaningful relationship with other variables such as total absorbed solar radiation by planets or the amount of greenhouse gases in their atmospheres. In other words, pressure is the only accurate predictor of NTE (i.e. ATE) we found. This fact appears to have completely escaped Mr. Eschenbach’s attention.
From Eq. (7) we derive our Equation 8 (the subject of Eschenbach’s analysis) in the following manner. First, we solve Eq. (7) for Ts, i.e
Secondly, we substitute Tgb for its actual expression from Eq. (2) to obtain:
Thirdly, we combine the fixed parameters 2/5, αgb, ϵ and σ in Eq. (7b) into a single constant, i.e.
Fourth, we use the newly computed constant along with the symbol NTE(Ps) representing the EXP term of Eq. (7b) to write our final Eq. (8):
Basically, Eq. (8) is Eq. (7b) expressed in a simplified and succinct form, where NTE(Ps) literally means the ATE factor as a function of pressure!
Let’s now look at how Mr. Eschenbach interprets Eq. (7) and its relationship to Eq. (8). He correctly identifies that Eq. (7) has 4 ‘tunable parameters’(the correct term is regression coefficients, but never mind this minor terminological inaccuracy for now). He then espouses:
Amusingly, the result of equation (7) is then used in another fitted (tuned) equation, number (8).
This is the first demonstration of misunderstanding in his analysis (with far reaching consequences as discussed below), where he fails to grasp that Eq. (8) follows simply and directly from Eq. (7) after a few straightforward algebraic rearrangements, and that it contains no additional tunable parameters! Instead, Mr. Eschenbach smugly informs our fellow bloggers that the constant 25.3966 is yet another tunable parameter, which he labels t5 (his Eq. 8sym)?! We point out that the fixed parameters used to produce this constant have been defined and set prior to carrying out the regression analysis that yielded Eq. (7). Indeed, it could not have been any other way, because these parameters are required to estimate the PGB temperatures (Tgb) used in the calculation of NTE values, which are subsequently regressed against observed pressure data. Thus, Eschenbach now leads the readers astray telling them that we use 5 tunable parameters instead of 4. Fascinating! Next, in a state of total confusion, he makes the following stunning proposition:
We can also substitute equation (7) into equation (8) in a
slightly different way, using the middle term in equation 7. This
yields:
Ts = t5 * Solar^0.25* Ts / Tgb (eqn 10
What middle term? This twisted line of reasoning is astounding, because it reveals an utter misunderstanding of basic algebra compounded with an inability to follow content, thus leaving the reader literally speechless! This error leads Eschenbach to his central false claim that our Eq. (8) simply meant Ts = Tgb * Ts / Tgb, and therefore reduces to Ts = Ts!? One can only stand in disbelief before such nonsense! This is what Mr. Eschenbach jubilantly calls ‘the sting in the tale‘. It is a big sting, alright, but in his tail, not ours! He proudly reiterates this ‘finding’ once again in the Conclusion section of his article leaving no doubt in reader’s mind about his analytical ‘skills’.
Blinded by a profound misunderstanding, Mr. Eschenbach pompously concludes in regard to the constant 25.3966 that what we have done is “estimate the Stefan-Boltzmann constant by a bizarre curve fitting method”. He further states: “And they did a decent job of that. Actually, pretty impressive considering the number of steps and parameters involved”. Wow! Hands down, such a conclusion could easily qualify for the Guinness Book of Records on Miscomprehension!
The rest of Eschenbach’s ‘revelations’ in regard to our Equations (7) and (8) are less flamboyant but equally amusing. He argues that the small constant cs in Eq. (2) is pointless while failing to understand the physical realism it brings to the new model (Eq. 8). Since the goal of our research was not just to derive a regression equation, but to develop a new physically viable model of the ‘Greenhouse Effect’, this constant is important in two ways: (a) it does not allow the PGB temperature to fall below 2.725K, the irreducible temperature of Deep Space, when So approaches zero; and (b) it enables Eq. (8) to predict increasing temperatures with rising pressure even in the absence of solar radiation. Indeed, if we set cs = 0.0, then Eq. (8) would always predict Ts = 0.0 when So = 0.0 regardless of pressure, which is physically unrealistic due to the presence of cosmic background radiation.
A major portion of Eschenbach’s criticism focuses on the ‘accusation’ that all we had done is just ‘curve fitting’ devoid of any physical meaning. In an Update to his article, Eschenbach attempts to prove that he can do a better job in fitting a curve through our planetary NTE values using an equation with fewer free parameters. His simplified version of our Eq. (8) has 3 regression parameters (instead of 4) and reads:
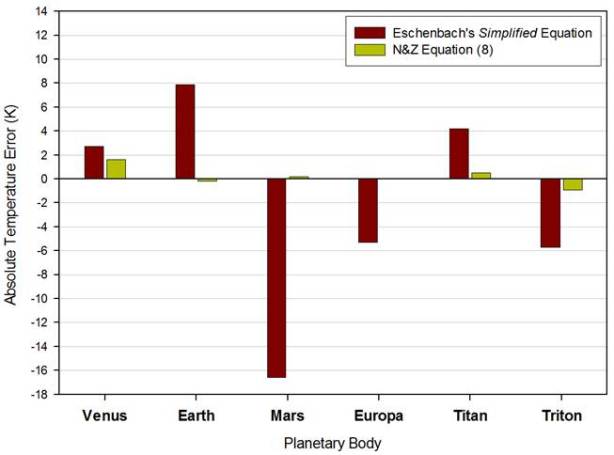
Figure 1. Absolute errors of predicted planetary mean surface temperatures by Eschenbach’s simplified equation and by N&Z’s Equation (8). Errors are assessed against the observed mean surface temperatures listed in Table 1 of Nikolov & Zeller’s original paper.
Note that his expression is in a sense more empirical than our Eq. (8), because the coefficient in front of So has been erroneously treated as a tunable (regression) parameter, hence distorting our PGB Eq. (2). Figure 1 compares the absolute deviations of predicted planetary surface temperatures from their true values (listed in Table 1 of our original paper) using Eschenbach’s regression equation and our Eq. (8). It is obvious to a naked eye that Eschenbach’s formula produces far less accurate results than our Eq. (8). This was also recently quantified statistically by Dan Hunt in an article published at the Tallbloke’s Talkshop. For example, Eschenbach’s equation predicts Earth’s mean temperature to be 295.2K, which is 7.9K higher that observed. This is not a small error, because the last time our Planet was 7.9K warmer than present some 40M years ago the earth surface was ice-free, and Antarctica was covered by subtropical vegetation! Of course, being a construction manager, Mr. Eschenbach likely has a limited understanding of Earth’s climate history and what a 7.9K warmer surface actually means. However, the fact that he claims aloud a superior accuracy of his simplified equation over ours is puzzling to say the least. His exact words were:
Curiously, my simplified version actually has a slightly lower RMS
error than the N&Z version, so I did indeed beat them at their own game. My
equation is not only simpler, it is more accurate
This statement blatantly contradicts the evidence. Mr. Eschenbach does not know that we have extensively experimented with exponential functions containing various numbers of free parameters many months before he became aware of our theory, and we have found that it takes a minimum of 4 parameters to accurately describe the highly non-linear relationship between NTE and surface pressure (Eq. 7). The basic implication of Eschenbach’s analysis is that one could indeed use a 3 parameter exponential function to predict planetary temperatures from solar irradiance and surface pressure but with far less accuracy. Truly enlightening!
By the way, curve fitting is an integral part of the classic science method. When dealing with an unknown process or phenomenon, taking measurements and using the data to fit curves is the only feasible approach to understand and develop a theory about the phenomenon. This method was extensively used throughout the 18th and 19th Century and a good part of the 20th Century to extract the so-called first principles in physics we currently employ to describe the World. However, arguing about curve fitting really misses the main point of our study.
Focusing on the Big Picture
What Mr. Eschenbach and a number of others have totally failed to grasp is the highly significant fact that the enhancement factor NTE (i.e. the Ts / Tgb ratio) is indeed closely related to pressure, and that no other variable can explain the interplanetary variation of NTE so completely. As Dr. Zeller pointed out in a recent blog post, given the simplicity of Eq. (8), it is a ‘miracle’ how accurately it predicts surface temperatures of planets spanning a vast range of environmental and atmospheric conditions throughout the solar system! This cannot be a coincidence! Rather it suggests the presence of a real physical mechanism behind the regression Equation (7) related to the thermal enhancement effect of pressure. This effect is physically similar (although different in magnitude) to the relative adiabatic heating observed in the atmosphere and described by the well-known Poisson formula derived from the Gas Law (see discussion in Section 3.3. and Fig. 6 in our original paper).
Even the mistaken analysis of Mr. Eschenbach could not manage to negate the above truth. He vigorously criticized our Eq. (8) using all sorts of faulty technical arguments only to arrive himself at a similar (albeit less accurate) equation that predicts planetary temperatures as a faction of the same two variables – solar insolation and pressure! His argument that one could arbitrarily use air density instead of pressure is groundless, because pressure as a force is the primary independent variable in the isobaric thermodynamic process of planetary atmospheres. Ground pressure depends solely on the mass of air column above a unit surface area and gravity, while air density is a function of temperature and pressure. In other words, density cannot exist without pressure. For a given pressure, the near-surface air density varies on a planetary scale in a fixed proportion with temperature, so that the product Density*Temperature = const. on average, i.e. higher temperature causes lower density while lower temperature brings about higher density according to the Charles/Gay-Lussac Law for an isobaric process.
We now draw attention to a key logical contradiction in Mr. Eschenbach’s approach. In the main text of his article, he makes the central claim that our Eq. (8) represented a mathematical nonsense, since according to his logic, it reduces to Ts = Ts (the TA-DA! moment). Yet, in the Update section, he uses data from Table 1 in our original paper to derive a very similar equation, which he calls a ‘simplified version’ of Eq. (8). So, according to Mr. Eschenbach, our Eq. (8) is numerically meaningless, while his equation based on the same data is mathematically sound. This raises the question, how poor do one’s reasoning skills have to be in order for one to contradict himself in such a ridiculous manner? We will let you be the judge …
Conclusion
We have shown in this reply that all criticism of our Equations (7) and (8) by Mr. Eschenbach is without merit. We emphasized the need for better understanding of and focusing on the big picture that our theory conveys. We propose to shift the discussion from meaningless argumentations about number of regression coefficients or number of significant digits of constants used, to how pressure as a force controls temperature and climate. In this regard, we would like to issue an appeal to all of you, who are capable of carrying out an intelligent discussion at a decent academic level to stop engaging in pseudoscientific, besides-the-point fruitless debates. We are here to discuss and offer a resolution to the current climate science debacle and welcome everyone who shares that goal. We are not here to promote or engage in endless circular talks or teach laymen ‘skeptics’ basic math and high-school level physics. Hence, we will no longer participate in dialogs of the kind that prompted this reply. We urge all sound thinking readers to do the same.
Thank you!
Tallbloke's Talkshop 
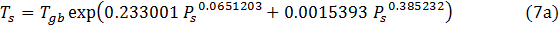
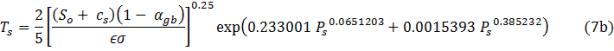
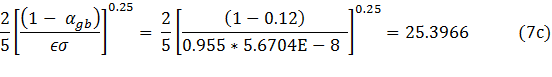
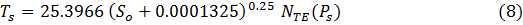
To All,
Please, realize that this entire discussion about regression coefficients and their ‘physical meaning’ pointless, because it does nothing to refute or negate the very EXISTENCE of the relationship.
This relationship is not a coincidence, because: (1) There are no other atmospheric parameters (besides pressure) that can explain (describe) so accurately and beautifully the variation of the empirically based NTE factor (the relative ATE) across planets; and (2) The shape of this relationship matches the response of the relative adiabatic heating to pressure changes described by the Gas-Law based Poisson formula… And that is the BIG PICTURE!
Lucy,
See my post above for answer to your question:
Lucy,
It was a log/log plot we used the derive Eq. 7. A log/log plot does not make the NTE – pressure relationship linear. It makes it somewhat less ‘exponential’ and less non-linear. We will present this plot in our Reply Part 2 …
Dr Nikolov says above
“We have already done this! In fact, the regression constants in our Eq.7 were derived from a plot of ln(Ts/Tgb) vs. ln(Ps) that did NOT include Titan, Moon and Mercury (we have not explicitly stated this in the paper). You can reduce the number of points (planets) and still get a very similar response function as long as the planets included in the regression span more or less the the whole environmental range. I think using Venus, Earth, Triton ans Europa will produce a function that very closely predicts the mean temperatures of Mars, Titan, Moon and Mercury. Try it …”
but this makes no sense – Mercury and the Moon have no atmosphere, and therefore do not contribute to the pressure dependence fitting anyway, so to say that excluding them makes the predictions more robust seems unlikely.
By the way, it would be helpful if the experimental sources for the temperature, pressure and density were given in detail. Half the planets being considering have never had any sensors landed, so all measurements are remote spectroscopic techniques – it would be interesting to see which methods were used to determine the data.
B_Happy says (February 14, 2012 at 9:43 pm):
but this makes no sense – Mercury and the Moon have no atmosphere, and therefore do not contribute to the pressure dependence fitting anyway, so to say that excluding them makes the predictions more robust seems unlikely.
Think, B_Happy! The regression curve describes a CONTINUUM from an airless surface to whatever pressure. Also, technically Moon and Mercury some small pressure: 1E-9 Pa …
Dr Nikolov
I can think and I know that a planet with zero pressure is taken care of purely by the exponential form of your equation. No fitting is needed therefore they do not contribute. It does not matter what parameters you have in your NTE factor, you will get the same answer for Mercury and the Moon no matter what. So can you explain again how they contribute to the fitting process, and thus how leaving them out proves anything?
Ned,
I see your point, but B_Happy’s also. I would suggest putting the airless and near airless bodies aside. Split the remaining ones into two groups and use the data from one to predict the data from the other and vice versa. It isn’t that the airless bodies don’t have value in the larger analysis, it is just that taking them out removes what will otherwise be a major objection. wars are won one battle at a time.
davidmhoffer February 9, 2012 at 6:39 pm refers to a past WUWT article that
Got a reference?
Lucy;
This is the paper I was referring to. “non stationary effects” are the ripples on the surface of the lake.
Fellows,
There is NO experimental evidence from the free atmosphere that increasing CO2, water vapor or any other so-called ‘greenhouse gases’ has ever caused an increase in temperature. We have proxy records of CO2 and global temperature going back more than 65M years. These data sets show that CO2 has ALWAYS lagged temperature changes. The CO2 time lag increases exponentially with the time scale of the data set considered. Thus, we find an 800-1,000-year lag in the ice core data covering past 1M years, and a 12.25M-year lag in the ocean sediment records covering past 65M years …
The whole notion that CO2 changes can affect global climate comes from models and models ONLY! Such effect is predicted by the climate models due to decoupling of radiative transfer from convective heat exchange in their code. In other words, the CO2 warming effect is a result of a physical algorithmic error in climate models, it’s a model artifact with no physical equivalence!!
Ned points out that it is nonsense to say that CO2 is a major factor controlling global temperature. The physical evidence shows that the temperature is a major factor determining the CO2 concentratration.
So why is it that the “Scientists” who are prepared to sell their souls claiming that CO2 rules are showered with money while their opponents find it hard to get funding?
I’m having a very enlightening experience, re-re-reading material here. I can only take so much science and formulae at a time. But repeated study here is like slowly clearing a frost-covered windscreen.
Early on with N&Z my instincts said YES!!! I was lucky to have just read about Jericho below sea level seriously hotter than nearby Jerusalem, and to have thought about the flat snow line on the hills and the cloud underside flat lines. And I was highly upset with Willis. So I was in the mood to study, always my solution to emotional upset is to re-examine the evidence. I was thus ready to take on the huge, under-our-noses paradigm shifter that atmospheric pressure is the major determinant of temperature. So obvious in hindsight.
Taking on the full power of N&Z, and the full weight of the maths and their fivefold paradigm shift, is taking much longer. But each time I re-read, the misty surface over comments here has cleared a little, patch by patch, as it were, and every time it’s been reinforcing N&Z, and suggesting to me that most of the commenters here are having similar experiences to my own. For some, the frost over N&Z has simply never lifted at all – especially those who feel emotionally uncomfortable with the presence of significant correlation, but with maths factors raised to strange fractions of powers, lack of recognizable patterns of causation.
Heck, this is how every major scientific discovery is made. We’re at the exciting moment when it’s clear the hunt is up, so let’s go looking for the causation. And on reflection, I suspect that N&Z suspect the fractionality has to do with things like convection – and this is why they consider convective influence in their equations.
At one point I thought that Huffman was right to criticize N&Z about albedo. But now I see where N&Z are coming from on this paradigm-shift too, I can also finally see that Huffman is wrong in every point he makes here. And now that I can see it, it doesn’t even look that difficult to see!
Ah, this is the problem. Communication. Especially when there are so many commenters one has to skim. Now that I understand N&Z better and better, even their communication sounds clearer and clearer. But I have to remember what it was like when I was a dummy, when all the words here were simply covered with white frost….
************************************************
Looks like I’ve finally found my elevator speech.
Lucy,
Great to hear that our concept is coming nicely into focus for a non-scientist and a math-shy person such as yourself. This means that hopefully other people will start getting it too … It’s really not a difficult paradigm to understand, but it does require a shift in perception. Once the shift is made, it becomes self-evident.
Now, go ahead and present your ‘elevator speech’ to Willis … you may have to do it in the elevator of the Empire State Building, though … 🙂
To gallopingcamel (February 15, 2012 at 1:23 am):
The CO2-based ‘theory’ of climate change might enter the Guinness Book of Records one day as the one supported by the least amount of empirical evidence, while violating the most fundamental laws of physics, yet being the longest lasting and most funded misconception in modern science … 🙂
When all the ‘dust’ settles down in 10-15 years from now, a major lesson learned from this gigantic Greenhouse blunder would be that any absurdity can be sold as a solid science for decades given the right amount of money invested in it.
Ned Nikolov says:
February 15, 2012 at 12:48 am
“The whole notion that CO2 changes can affect global climate comes from models and models ONLY! Such effect is predicted by the climate models due to decoupling of radiative transfer from convective heat exchange in their code. In other words, the CO2 warming effect is a result of a physical algorithmic error in climate models, it’s a model artifact with no physical equivalence!!”.
Obervations show we can ignore radiative effects such as IR absoption.Mass not composition determines the temperature of an atmosphere.That what you say.
Also the thermodynamic theory of a gases( gas laws) confirms this.
Within the atmosphere radiative transfer is decoupled from heat exchange ( conduction and convection ).
Radiation ( light) is a property of space, heat and all other forms of energy are properties of matter.
How is this possible? Maybe the total matter ( mass) of the atmosphere absorbs and emits radiation such that the heat energy and also the radiation energy each stay the same.
TO: Roger Clague (February 15, 2012 at 9:47 am)
I would like to clarify something important. I am NOT saying that “within the atmosphere radiative transfer is decoupled from heat exchange ( conduction and convection ).”… On the contrary, in the REAL atmosphere radiative transfer is coupled to (happens simultaneously with) convection! Since convection is MUCH more efficient than radiation in transferring heat, globally, it completely offsets on average the warming effect of back radiation. So, the long-wave back radiation does NOT heat the surface in reality…
In climate models, however, radiative transfer is NOT solved simultaneously with convection. As a result, changes in atmospheric emissivity (due to an increase of CO2 concentration for example) lead to the calculation of positive heating rates (degree per day). These rates are produced by the radiative transfer code due to the fact that it is solved independently (outside) of convective processes. The heating rate predicted by the radiative transfer code are then passed onto the thermodynamic (convective/advective) portion of the model, and get distributed around the globe causing the projected warming. So, it is this ARTIFICIAL decoupling between radiative transfer and convection in climate models that is responsible for the non-physical prediction of rising surface temperatures with increasing atmospheric CO2 concentration.
Ned: So, it is this ARTIFICIAL decoupling between radiative transfer and convection in climate models that is responsible for the non-physical prediction of rising surface temperatures with increasing atmospheric CO2 concentration.
That is the trouble with modeling processes is it not. In systems such as the climate that are constrained and driven by so many multiple physics equations and laws that ALL are occurring simultaneously and they all are also inter-related, each affecting the others ruling parameters recursively. Let’s face it, we will never match nature’s calculations, her ‘computer’ has hundreds of digits of precision and a Δt better that yocto-seconds… that is the core reason that predicting the future in such of a system of more than days or maybe weeks is pure fantasy.
Wayne, I would not take Dr Nikolov’s word for it that convection and radiative transfer are decoupled. These models treat the earth’s atmosphere/ocean/ice caps as a 3D grid (ie a set of boxes) and each box influences its neighbours both spatially and in time ie the calculations of pressure and temperature etc in one box at one time are fed into the calculations of the pressure etc of both that box and its neighbours at the next time step. Does that sound to you as if they are decoupled? Now you could argue that they have the magnitudes of some of the couplings (a.k.a feedbacks) wrong, and that makes the models inaccurate (and I would probably agree with that), but that is an entirely different assertion to claiming that the couplings are missing entirely.
N&Z have not responded to my post so I will try it again – I think it shows up some serious errors in their application of Hölder’s inequality
Their Equation 2 seems to sum TSI and Cs then spread it round the globe. However Cs is already global so should not be so spread it must be constant over the surface. Inconsequential but physically wrong.
I do not see where the continuous downwelling radiation is handled in the equations. Like Cs this is day and night 200+ watts so should not be spread equatorially although it does taper off polewards.
the 200Watts was measured here SGP Central Facility, Ponca City, OK 36° 36′ 18.0″ N, 97° 29′ 6.0″ W Altitude: 320 meters
Eq 3 uses ap= Earth’s planetary albedo (≈0.3).
Eq 2 uses agb=Earth’s albedo without atmosphere (≈0.125),
Why the difference both assume atmosphereless planet?
[co-mod: I think the answer will come with Part 2 which N&Z have not yet posted. They are trying not to get too distracted at the stage, hence some patience is needed. –Tim]
B_Happy;
each box influences its neighbours both spatially and in time ie the calculations of pressure and temperature etc in one box at one time are fed into the calculations of the pressure etc of both that box and its neighbours at the next time step. Does that sound to you as if they are decoupled?>>>
To be fair, I don’t really know how the models work, I have never dug into it in detail. That said, I have a simple question:
Given that the models get it wrong, have no hindcast capability, no predicitve capability, and have repeatedly been shown not just wrong, but way wrong, if Dr Nikolov’s explanation of why isn’t correct, then what IS the reason?
Keep this in mind as far as GCM are concerned. I read it as the models are less than 3D
http://declineeffect.com/?page_id=189
“Given that the models get it wrong, have no hindcast capability, no predicitve capability, and have repeatedly been shown not just wrong, but way wrong, if Dr Nikolov’s explanation of why isn’t correct, then what IS the reason?”
Well that is probably a bit of an exaggeration, but I agree that the models are not satisfactory. I am not a climate scientist by the way – I work in a branch of physical chemistry which also uses a lot of computer time and shares a few techniques, but I deal with system about 10^12 times smaller!. I would say that the current GMC’s are interesting as scientific explorations, but do not have the accuracy needed to justify the kind of political and economic decisions that they are being used to support. As for what I think is wrong, well that was alluded to above.
They are trying to use the Navier-Stokes equations, which model flow in gases, and solve them using a multi-grid, multi-timestep approach. Multi-grid because they need different size ‘boxes’ for atmosphere and ocean, and multi-timestep because these evolve at different rates. So they have a whole set of coupled partial differential equations that they are evolving in time, but not all of the couplings (feedbacks) are known accurately. The trouble with this is that the errors can (in fact do) build up over time i.e if there are inaccuracies on a particular time step, then these are fed into the next time step along with the parts that are right. Eventually you can end up with nonsense. The particular coupling that are worst described are those linking temperature, humidity and albedo, which are called clouds by most people…
However saying that the couplings are wrong is not the same as saying that there are no couplings – the latter statement is incorrect.
B_Happy says:
February 15, 2012 at 10:56 pm
Wayne, I would not take Dr Nikolov’s word for it that convection and radiative transfer are decoupled.
B_Happy, are you are climate modeler or have you worked with climate models at all? This is not my word, but a fact! Allow me to know my field, please!
Yes, climate models are 3D models, but that refers ONLY to the thermodynamic part of the models. Radiative transfer (RT) code works in 1D (along the vertical axes) only, and RT calculations are performed NOT at every time step, but at every OTHER time step of these model. Also, RT is not solved in the same iteration with convection. Rather it is solved independently at a given time step, and it’s results in terms of heating rates are then passed to the 3D thermodynamic portion of the model …
” but at every OTHER time step of these model”
In other words they are coupled…..do you not know what this means?
B_Happy, Hoffer beat me to it… no hind cast capability. I also have not taken the time to dig into climate simulations either but I have written multiple solar system simulators where you have something as simple as the 15 most massive bodies all interacting simultaneously. That’s 210 3d ODE projections per small dt of a sixth order integrator (position –> velocity’, acceleration”, jerk”’, snap””, crackle””’, and pop””” derivatives :)) and the accumulating round-off error will always get you in the end.
I do know the problem nice and personal. Just as a dreamed up example to illustrate… to me a simulator is only marginally ‘correct’ if you can run it backward let’s say 600 years and tell within a few arc-minutes that an osculation matches to the monk’s records in English adjusted France’s Julian 1413-Apr-7 at 3:10 am local time of x-star by y-planet. And not relying on one exact confirmation but hundreds. Then, and only then, do you know that if you then reverse the integration can you somewhat trust it’s accurately predicting positions and times in the near future. Climate simulations have a long, long ways to go, if they are ever even possible. That is why I will not spend my time on climate simulations. Far, far to many assumptions, to much questionable data, to many inter-tangled physics limits and processes, some of the physics is questionable itself… mother nature always knows reality… we never will. It is a fantasy and I don’t have time for pure fantasies. I’d rather write a fantasy game, at least then I would understand that it is only fiction.
Once climate models can, in reverse, match the monthly records backwards for something like 20 years tit-for-tat I’ll have more confidence in their ability to possibly predict the near future. So far, two years ago, they can’t even match last years temperature records.
That’s how I see it.
Wayne,
That is more or less what I said. I was not claiming the models were accurate, just that they were not inaccurate for the reason Dr Nikolov was stating, since he is actually wrong on that specific point.
From sun to the top of the atmosphere radiation rules, we ignore matter. However climate models include both radiative tranfer and heat transfer, coupled or not.
Observations shows that thermodynamic gas laws alone explain the properties of atmospheres.
We assume at TOA that radiation in is equal to radiation out. Radiation produces heat and hot things radiate but the but the effects cancel each other.
Climate models should be purely thermodynamic not a mix of radiation in space and heat tranfer in matter.
B_Happy, OK. I’d still pay heed to what Ned was saying. I believe he is correct and I myself have a major nit to pick with the radiation code within then models and Trenberth among others’ handling of radiation, the one dimension aspect. But it will take a while to compose a proper explanation so check back here later, like tomorrow evening, maybe even Friday. The handling in radiation in all of climate science is messed up and everyone can properly feel it, the numbers never jibe and I think I have found the reason.
I’d be grateful if Ned would add any further clarification he feels is needed to this post – I didn’t get a reply from him in time to add it here.
Joel Shore says in an unapproved comment:
tallbloke:
Congratulations on [snip] so that Nikolov’s [snip]. This statement by Nikolov is [snip]: “The whole notion that CO2 changes can affect global climate comes from models and models ONLY! Such effect is predicted by the climate models due to decoupling of radiative transfer from convective heat exchange in their code. In other words, the CO2 warming effect is a result of a physical algorithmic error in climate models, it’s a model artifact with no physical equivalence!!”
In fact, nobody (including N&Z) has challenged my content[ion], which is[;] the reason why N&Z got rid of the radiative greenhouse effect by adding convection is that they added it in totally incorrectly. We know that because they tell us they added it in incorrectly when they say, “Equation (4) dramatically alters the solution to Eq. (3) by collapsing the difference between Ts, Ta and Te and virtually erasing the GHE (Fig. 3).” I.e., they tell us that they added in convection in a way that leads to the completely unphysical result of an atmosphere isotropic with height, i.e., with zero lapse rate. And, any elementary climate science book would tell them that this would indeed eliminate the radiative greenhouse effect.
I guess you are trying to make your site the place on the internet where [snip]
[Reply] Hi Joel, thanks for vindicating my reasons for preventing you from turning my blog into a ruckus of inflammatory comment, misdirection and unjustified accusation.
N&Z say:
“Pressure by itself is not a source of energy! Instead, it enhances (amplifies) the energy supplied by an external source such as the Sun through density-dependent rates of molecular collision.”
So the temperatures nearer the surface where the atmosphere is under greater pressure and the density of the compressible air are higher than those at high altitude, in a proportion which approximates to the observed lapse rate. The pressure and consequent thermal gradient is not included in equations 3 and 4 because it is not required for the purposes of demonstrating the inadequacy of radiative activity to account for the GHE (or the lapse rate), this is why the conceptual system under consideration is isotropic.
Karl Zeller adds:
” Rog, we are only showing the impact of adding convection on a ‘thin-slice’ one-dimensional model to demonstrate the effect. We go on to say: ‘These results do not change when using multi-layer models. In radiative transfer models, Ts increases with ϵ not as a result of heat trapping by greenhouse gases, but due to the lack of convective cooling [in the radiative transfer models], thus requiring a larger thermal gradient to export the necessary amount of heat.’
Cheers
Rog
I’ll add the publishable parts of Joel’s next reply plus any further response necessary after the weekend.
[…] Shoulder to Shoulder with Anth…BenAW on David Hoffer: Short Circuiting…tallbloke on Nikolov & Zeller: Reply to…davidmhoffer on David Hoffer: Short Circuiting…wayne on Nikolov & Zeller: Reply […]
Dear Dr. Nikolov,
Thank you for the courtesy of a serious reply. Allow me to address your points one at a time.
1) I have no problem with your expressing the GHE or ATE as a dimensionless ratio.
2) I do not mean to suggest that
in your paper is arbitrary. However, in computing it you use a single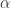 
for the Earth and for the Moon and for Europa and for Venus, but this number bears no resemblance to their actual bond albedo. Unless you consider the solid high albedo “ice” (in the case of Triton N_2 ice) coating nearly atmosphere-free Europa and extremely diffuse atmosphere Triton this doesn’t make the slightest bit of sense. The entire point of the insolation computation is to determine the fraction of solar energy that heats the planet and must ultimately be lost through radiation. The whole point of the albedo in this computation is that it is a direct measure of the fraction of energy reflected away without causing heating. Why bother with albedo in the first place if you’re going to do this?
I’ll tell you why. Because by doing so, it becomes an irrelevant scale factor — you’ve eliminated a source of variability for the planets. You can indeed factor
(and all the other constants) out from under the integral in your equation (2), and write 
where C is a constant for all the planets and 
is the TOA TSI for the planet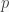 
. When you form the dimensionless ratio 
, the constant simply doesn’t matter as it no longer contributes to the variability and you’ve made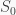 
the only variable. This is just a projection technique, in other words.
It introduces significant errors into your table 1 number for
. The data in this table has other problems. When I look for the bond albedo of Venus (for example) in actual publications such as:
http://www.sciencedirect.com/science/article/pii/S0019103505005105
I get 0.9, not 0.75, and you do not provide anything but “multiple references using cross-referencing” which makes it hard for me to assess whether your number is likely to be better. In this case
and the error associated with ignoring the true bond albedo in favor of an artificial one that turns 
into a direct proxy for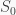 
could be as high as 43%.
In the end, the reason it doesn’t matter much is the forgiving nature of 1/4 powers, and yes I understand that
is always an artificial measure, but it doesn’t help to have you do a better job of computing it by accounting for spherical geometry and 
and then a worse job of handling the albedo without any estimation of errors!
Still, I appreciate what you are trying to do, so let’s just let this go for the moment and concentrate on the rest of it. Bear in mind that I am being critical but I am not hostile to your efforts. Indeed, I agree that the “33 degree warming” number is bullshit, think that in general your improved formula for computing
is an improvement, although it would be improved still more if you didn’t insist on making every planet into the Moon as far as albedo is concerned. I also think there is still more work to be done here, because I do not agree with some of your remarks (made in other papers of yours I’ve grabbed) on just how to compute an average surface temperature for the purposes of considering outgoing radiation. But we can discuss this (if you like) another time.
3) Our analysis revealed that mean surface total pressure (Ps) is the only parameter that nearly completely explains the ATE values for all 8 planets. No other parameters such as ‘greenhouse-gas’ concentrations or their partial pressures, or the actual absorbed radiation by planets (accounting for observed albedos) came even close to describing the ATE variation. Hence, the derivation of Eq. 7. Again, NTE(Ps) was derived using non-linear regression!
Before I start on the substance of this, let’s get one thing straight. One does not “derive” an equation using regression. One fits data to a presumed functional form using regression. One derives an equation by using the laws of physics, algebra, calculus, geometry, things like that. If you want to be picky, one derives theorems from axioms, but in physics a “derivation” invariably means proceeding from the axioms of physics — the laws of nature, or accepted idealized empirical formulae that themselves may or may not be derived — to a result.
For contrast, you arguably derived your variant (2) of the usual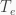
formula — you could have provided a lot more detail, but what you provide is enough for me to see what you are doing, and since I already have a good idea of where 
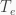comes from I can at least assess whether or not I agree with your derivation, whether you did your spherical integrals correctly, and I can identify where I do not agree, e.g. using a one-size-fits-all albedo that completely defeats the purpose of this idealized measure of the integrated absorbed power. In my opinion, of course. The sunlight directly reflected from Europa’s shiny white surface does not contribute to its surface temperature.
On the other hand, you did not even justify the form of the function(s) used in your fit using physical laws, and when I point out that it contains implicit physical constants (the pressures required to make the arguments dimensionless) that cannot possibly be justified — again, in my opinion, but feel free to prove me wrong — you loudly ignore this. So please, do not assert that you have derived equation 7 or 8. It isn’t even semi-empirical, it is purely empirical and ad hoc.
Next let’s think about your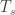
data in table 1. You provide it, and 
, and just about everything in your table, to absurd precision. Do you seriously mean to assert that the Earth’s mean temperature is exactly 287.6 K? Has this temperature historically been constant? Even for the Earth, surely the best measured body in the Solar system, there is considerable argument over just what the average surface temperature is (much of it on this very blog) and it varies by at least 10K (3%) over time scales as short as a few thousand years.
[Parenthetically, if your equation 7 were truly predictive, how would it predict this? Are the ice ages caused by the Earth losing atmosphere and hence surface pressure? Do they end because the pressure goes up?]
[Reply] Don’t forget the other half of the equation – Insolation, the distribution of which changes considerably with the changes of obliquity, precessional orientation and orbital eccentricity the earth undergoes on these timescales. – TB.
It has varied by over a degree on a timescale of a mere 100-150 years. Surely “288 K” would do for the temperature, and “287 +/- 2” K would be a better descriptor still on the timescale of centuries, given that we are probably at a local high point.
Or perhaps not. Perhaps you have a source that you rely on to give you more than an uncertain measure of the Earth’s temperature, one with error bars and without tenths of a degree. If we assume (reasonably) that the order of uncertainty in the Earth’s temperature is 1%, surely the order of uncertainty in all of the other planets with the possible exception of the Moon is an order of magnitude greater.
Maybe you disagree. Maybe you can cite references to support the temperatures you give in this table, and a claim that they are known right down to that last 0.1 degree, although I can’t imagine that our fundamental sources are different for the outer moons, just about all of which are known only from one or two flybys of satellites. However, you have not given any references at all to support the data in table 1, so I cannot assess this. Wikipedia has better referential support than this paper for its data.
To pick just one more entry in your table 1, Europa, Wikipedia indicates that it has an equatorial average temperature around 110K and a polar average temperature around 50K. You indicate an average surface temperature of 73.4K. Yet one does not have to do the integrals to see that this is inconsistent with Wikipedia’s result. A straight arithmetic average of the two is higher than this, but there is much more surface area at the equator, due to the Jacobean you so ably included in your improved integral in equation (2). Guestimating the integral, the mean surface temperature should be closer to 90K, although this would still have a large error estimate, would it not, and there is no chance that could actually be accurate to 0.1 degree K.
Before I or anyone can consider the goodness, or uniqueness, of your fit to your data, surely one needs to have the probable or possible sources of error accounted for and error bars included in the numbers for use in the regression program. One can get truly horrible errors fitting a set of noisy data with a single one size fits all error bar (especially one that is too small so it places too much weight in the fit on data that is actually not known particularly accurately, even more so when one is fitting a small set of data with a large set of parameters). In the meantime, as I said, fit the data with a cubic spline — it is just as meaningful. What you’ve done is no different from Roy Spencer’s “cubic fit” presented on his lower troposphere temperature curve — presented a curve that smoothly interpolates the data, sure, but that is physically unmotivated and hence meaningless except as a guide to the eye. Spencer openly acknowledge it. You’ve written a paper on it, claiming that your arbitrary fit is “derived” by virtue of roughly interpolating the data.
Now let’s talk about Equation 7 itself. You yourself in figure 6 plot “potential temperature”. Potential temperature is a dimensionless quantity like the one you hope to understand in the form of
— I get it. Note well that in the case of potential temperature, because it is based on and indeed actually derived from some fundamental physics, the two numbers that appear: 
and the exponent $0.285$ are both entirely physical!. The one is a reference pressure that not only is relevant but sets the scale of pressure-temperature relationships for the entire atmosphere, the other is related to 
and the atmosphere’s actual molecular composition. This is characteristic of “good physics”, or at least of plausible physics. The quantities make physical sense even before one digs into and learns to understand where they come from.
For some reason you presented Equation 7, the result of your nonlinear regression fit, in a form that was not as manifestly dimensionless as potential temperature in figure 6, after claiming it as inspiration. I have helped you out there by filling in the characteristic pressures that go with your choice of exponents. These pressures are clearly absurd, are they not? Unlike
in potential temperature, 54,000 atmospheres is a pressure that appears nowhere in the physics describing ideal gases, in physical processes that might possibly be relevant on the surface of Europa or Triton or Mars or Venus.
I’ve played the “fitting nonlinear functions” game myself, for years, as part of finding critical exponents from scaling computations, and in the process I learned a thing or two. One thing I learned is that it is often possible to get more than one fit that “works”, and that the fit that works best may not be the one you are seeking, the one that makes physical sense. Often this is a matter of the error bars or lack thereof. Too small error bars will often “constrain” the best fit away from the true trend hidden in the data. The problem is compounded when one is fitting data with multiple independent trends, such as a fast decay mixed with a slow decay (multiple exponential).
Your data clearly has such multiple trends with completely distinct physics — you misrepresent it as a single fit, but presenting it in dimensionless form clearly shows that you are really proposing two different physical processes occurring at the same time with completely different characteristic dimensions. I think this is as clear a signal as you will ever see that you are overfitting the information content of the data, and would do far better to just fit the larger planets on your list with a single dimensionless form, preferrably after putting error estimates into all of the data in your table 1 and using the correct bond albedo for the planets in question, and adding references.
In summary, the tight exponential relationship between NTE and pressure is real, and the fact that it is described by a function, which coefficients cannot be easily interpreted in terms of known physical quantities, does not invalidate that relationship! This is because it is a higher-order emergent relationship, which summarizes the net effect of countless atmospheric processes including the formation of clouds and cloud albedo. This relationship might not be precisely reproducible in a lab, simply because it may require a planetary scale to manifest. However, a lab experiment should be able to validate the overall shape of the curve defining the thermal enhancement effect of pressure over an airless surface. BTY, this shape is already supported by the response function of relative adiabatic heating defined by Poisson’s formula (Fig. 6 in our paper).
Actually, as I’ve pointed out very precisely above, equation 8 is just as algebraic restatement of your definition of
. You’ve simply inserted an empirical heuristic fit to your data to replace the data itself. This isn’t a derivation of anything at all, it is curve fitting, which is a game with rules. Mann, Bradley and Hughes tried to play this game and broke the rules when they built the infamous Hockey Stick. Mckittrick and McIntyre called them on it.
I’m trying to keep you from making the same sort of mistake. You fit the data with the product of two exponentials of ratios of the surface pressure to arbitrary powers. Why? Well, exponentials are functions that are 1 when their argument is zero, so you fit two of your data points (badly if you leave out error bars or use the actual data in your table) for free without using a fit parameter, and come damn close to a third, close enough that — lacking error bars and given a monotonic relationship — you can count it as “well fit” whatever the error really is.
You then are really “fitting” five data points with four free parameters. Skeptics often quite rightly mock the warmist crowd for their global climate models with highly nonlinear behavior and enough free parameters that they can be tuned to fit past temperature data, accurate or not, as nicely as you please, and we are not surprised when those fits of past data turn out to be poor predictors of either future trends or even earlier past data (hindcast). We mock them because it is well known in the model building business that with enough free parameters and the right choice of functional shapes you can fit anything, but unless you treat error in the data with the respect it deserves and include some actual physics in the choice of functions being fit, the result is unlikely to actually capture the physics.
Listen, in fact, to your own argument. There is a dazzling amount of physics involved in the processes that establish the surface temperatures on the planets in your list. One can split the planets up into completely distinct groups — two airless planets near the sun with no surface ice, two nearly airless planets that are completely coated in high-albedo ice, one water ice, one frozen N_2, one of which is heated by a tidal process that still isn’t well understood, the other of which is hypothesized to have a greenhouse trapping of heat by the semi-transparent N_2 ice that replenishes its atmosphere. Of the four planets with substantial atmospheres all of them have an optically thick greenhouse gas content and all of them therefore have tropospheres and stratospheres and lapse rates driven by vertical convection across the temperature differential between the surface and the tropopause.
Yet somehow none of this matters? Calling it an “high-order emergent relationship” is just fancy talk for “we found a fit and have no idea what it means”, but it isn’t surprising that you can fit the data with an arbitrary form with four free parameters, especially without error bars or any criterion for judging goodness of fit.
How is your fit more informative than fitting the data with a spline, or with a polynomial, or with anything else one might imagine? I’ve already pointed out that your figure 6 is precisely why one should not believe your result. In it,
means something, and so does the exponent. There is nothing “emergent” about it, it is really a derived result, and when it turns out to approximately describe actual atmospheres we gain understanding from it.
What does the 54,000 bar in your fit mean? What does the 202 bar in your fit mean? What does the exponent 0.065 mean? You cannot answer any of these questions because you have no idea. How could you? They are all completely irrelevant to the pressures present on the planets in question. They have precisely as much meaning as the arbitrary coefficients of a cubic spline or any other interpolating function or approximate fit function that could be used to approximate the data, quite possibly as well or better than the fit that you found if you actually add in error bars
[Reply] In fact Ned has addressed your concerns regarding your oft repeated assertion, please revue his recent reply to you again. I’d also like you to answer my question which I’ll repost here:
“Please could Robert explain the physical basis of the imaginary number ‘i’ (or ‘j’ in engineering) the product of which when multiplied by itself is minus 1, which is used extensively in electronics design and control engineering? Presumably any competent Duke physicist at the time of the invention of this imaginary quantity which defies the laws of mathematics would have rejected it out of hand for being “absurd nonsense” and therefore of no possible use? – Thanks – TB. .
So far the total information content of your paper is:
* We do a better job of defining/computing a baseline greybody temperature
for the planets.
Yes and no. Yes to the integral, no to ignoring the bond albedo, especially in the case of Europa and Triton where there is no conceivable justification for doing so.
* We define a dimensionless ratio between empirical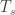
and 
. We tabulate this computed ratio for the data, forming an empirical 
dataset with eight objects.
Sure.
* We heuristically fit a four parameter functional form. The fit works. It is unique. It must be meaningful.
Lacking error bars on your data, you cannot possibly assert that it is unique. There could be dozens of functional forms, some of them with fewer free parameters, that produce comparable Pearson’s
for the fit once you add in error bars. I rather expect that there will be, especially if you correctly treat the bond albedo for planets with almost no atmosphere and no exposed regolith that reflect away over half their incident insolation without being heated by it.
The fit you obtain is not meaningful. If you disagree, give me a physical argument for the 54000 bar, the 202 bar, and the exponent of 0.065. The only parameter of your four parameter fit that is plausible is the 0.385, although even that number would need to be connected to some actual physics in order to obtain meaning.
* The real meaning is that only surface pressure explains surface temperature, because we were able to fit a functional form to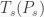
.
Excuse me? I can fit any set of data pairs with any sufficiently large basis. If the data is monotonic I can almost certainly fit it with fewer free parameters than there are data points, especially if I completely ignore the error estimates for the data points! Lacking the error bars, you cannot even compute
and plausibly reject no trended correlation at all! I’m not suggesting that this is reasonable for your particular data set, only that you are far away from presenting a plausible argument for uniqueness or correlation that implies causality. In two of the four planets in your list, it’s rather likely the case that surface temperature implies surface pressure, not the other way around! The chemical equilibrium pressure of N_2 over a thick layer of N_2 ice or O_2 over water ice is far more likely to be the self-consistent result of surface temperature, not its cause.
In the end, you are left where you started — that there is a monotonic trend to the data that you cannot explain or derive, and because of flaws in your statistical analysis you cannot even resolve difference between competing explanations including the simplest one that the last four planets have surface temperatures dominated by the greenhouse effect and their albedo, the first two are greybodys to a decent approximation (that somehow turned into 1.000 to four presumed significant digits in your Table 1), and two are special cases described by a completely different physics than the others (dominated by the incorrectly used albedo), and to some extend different even from each other.
Nothing in your analysis rejects this as a null hypothesis. You cannot even assert that it does without including an error analysis in your data and fit.
To conclude, you have two choices. You can ignore my objections above and plow ahead with your paper as is. You might get it past a referee, although I somewhat doubt it. You can in the process continue to get all sorts of uncritical positive feedback on it on the pages of this blog and have it trumpeted as “proof” that there is what, no actual GHE? That gravity alone heats atmospheres? I’ve heard all sorts of absurd punchlines bandied about, and your result can be used to support any or all of them if one ignores the statistical and methodological flaws.
Or, you can fix your paper. Include references, for example. Use the correct bond albedos. Here’s a small challenge for you. Apply your formula to Callisto, to Ganymede, to other planetary bodies. Callisto is an excellent case in point. It has an albedo almost twice that of the moon, It is the warmest of Jupiter’s moons — warmer in particular than Europa, for good reason given the difference in their albedos . It has an atmosphere with a surface pressure around 0.75 microPa, it will fit right in there on your table. It puts the immediate lie to any assertion that your fit is either predictive or universal, as its surface pressure is lower than Europas and its surface temperature is higher than Europas and if you use your “universal”
formula for it the lower albedo will further raise 
for it relative to Europa. Your nice monotonic curve won’t be monotonic any more, and you can see some of the consequences of ignoring albedo, atmospheric composition (Callisto’s is mostly CO_2, hmmm), error estimates, and using cherrypicked data to increase the “miraculous” impact of your result.
I honestly hope that you fix your paper. There may well be something worth reporting in there in the end, once you stop trying to prove a specific thing and start letting the data speak. I actually rather like what you are trying to do with
, but if you want to actually improve this you can’t just leave physics out at will, especially not when looking only at the temperature of moons tells you that your assumptions are incorrect even before you get to actual planets with actual atmospheres. Also, if you do indeed do your statistical fits correctly, you might find something useful — a less “miraculous” fit that is still good given the error bars and that has characteristic pressures and exponents with some meaning,
Best regards,
rgb
Oops, Tallbloke please insert my missing $. Sorry.
rgb
[Reply] No problem, please answer my question about the imaginary number I’ve re-inserted into your long comment as a return favour. 🙂
Robert Brown, you have not read N&K’s paper correctly. N&K’s Tgb has nothing to do with the actual atmospheric Bond albedo. Tgb is defined in the paper as the albedo and emissivity of that planet or body with NO atmosphere… no ice… no oceans… no clouds, possibly no rotation though in the definition that matters little. You start off incorrect in your point two from the very beginning. Now I’ll read the rest of your lengthy comment.
Tallbloke, you may want to find a better analogy. Asking about the physical basis of ‘i’ is the same as asking what the physical basis of the number 42 is. It is just a number unless it is being used in a specific context to represent something physical. In this case, as Dr. Brown has repeatedly noted, the construction of the N&Z equations puts the regression coefficients in a context that gives them a physical meaning (they have units of pressure).
Also, I would suggest to you that ‘i’ does not defy the laws of mathematics at all. It is just another abstract mathematical concept that is useful in solving some physically meaningful problems.
[Reply] Know of any other ‘numbers’ which when multiplied by themselves gives a negative number?
Dear Dr. Brown:
You have asked legitimate questions and we plan to address them all in our Reply 2. This would be better than addressing them here, because readers can then link those to the bigger picture discussed in Part 2. BTW, some of the answers have already been provided in the papers and in our blog posts on this and other threads, but we will elaborate on those once again since we understand that being a new paradigm, this theory has details that can easily escape one’s attention on a first read …. For example, to your question:
“… if your equation 7 were truly predictive, how would it predict this? Are the ice ages caused by the Earth losing atmosphere and hence surface pressure? Do they end because the pressure goes up?“.
The answer is partially contained in Section 5 of our first paper, and specifically in Fig. 10. Ice ages are NOT caused by pressure changes, they are caused by orbital variations (the so-called Milankovitch cycles). Earth’s atmospheric pressure has been relatively stable for the past 1.8M years. Pressure changes typically occur (and control global temperature) on a time scale on millions to tens of millions of years …
wayne says (February 17, 2012 at 12:01 am)
Robert Brown, you have not read N&K’s paper correctly. N&K’s Tgb has nothing to do with the actual atmospheric Bond albedo. Tgb is defined in the paper as the albedo and emissivity of that planet or body with NO atmosphere… no ice… no oceans… no clouds, possibly no rotation though in the definition that matters little. You start off incorrect in your point two from the very beginning.
Thank you, Wayne! You made quite a correct observation! … As I mentioned previously, a lot of details are not being picked up (understood) by many bloggers including physicists on the first read. That’s because people always look through the glasses they are used to wear, while a new paradigm requires a new pair of glasses … 🙂
[ 😯 ]…[ 🙄 😈 ]
N&Z propose a change of paradigm in “climate science”.
One of my favorite paradigm shifts was proposed by Alfred Wegener concerning his unproven “continental drift”, (tectonics), for which he was scorned by his contemporaries, only to be accepted relatively recently.
A controversial blogger “Myrrh” at WUWT has cited extensive links that convincingly explain WHY people living in areas of low exposure to sunlight by latitude have evolved to have pale skins, whilst being descendants of black peoples in Africa. The evidence is strong that that vitamin D is multiply essential for health, and that much more D is generated by UV in pale skin.
However, this flies in the face of the medical and governmental church, whom collectively insist that we should not expose our skin to sunshine.
See Myrrh’s post: http://wattsupwiththat.com/2012/02/03/monckton-responds-to-skeptical-science/#comment-895283
And my following response, but there is a lot of reading in the links which may not be time effective for N&Z to follow.
Thank you, Wayne! You made quite a correct observation! … As I mentioned previously, a lot of details are not being picked up (understood) by many bloggers including physicists on the first read. That’s because people always look through the glasses they are used to wear, while a new paradigm requires a new pair of glasses … 🙂
Dear Dr. Nikolov,
I assure you that I have not missed this point. However, it is completely irrelevant.
I have just completed applying your hypothesis, with your own numbers for T_gb per object, to the actual commonly accepted numbers for T_s for the planets in question. Curiously, with the exception of the last three points not a single planet lies on your curve. I have also applied your formula, with the T_gb you supply to objects orbiting Jupiter (e.g. Europa) to Io, Ganymede, and Callisto, all of which have even more atmosphere than Europa and all of which are considerably warmer — but not in the right direction — Io has the greatest surface pressure by three orders of magnitude but Callisto has the greatest mean temperature.
None of them — including Europa, whose mean temperature you underestimate by over 30% — lies remotely near your curve using your own T_gb. However, the warmer temperature of Callisto is instantly understandable given its low albedo.
This forces me to ask the question — exactly how did you come by the numbers in your Table 1 for T_s for the planetary bodies in question? When I look at the goodness of the fit to your model, it appears to me to be impossibly good. Literally impossibly. If one ascribes even modest error bars to the T_s and P_s in question, your curve would seem to put each and every point dead on the curve. Surely you realize that this is extremely unlikely in any fit involving real world data. You do not provide any references for the numbers in your Table 1 so I cannot check them against the references you actually used, but they are in significant disagreement with the numbers that I found in every instance but Titan, the Earth, and Venus.
One critical aspect of science is reproducibility. I am endeavoring to reproduce your results, but find myself unable to. Please help me by explaining the sources of your data and how you arrived at the numbers in your table 1.
I’d be happy to provide the table of numbers I used, and a description of their provenance, as well as the octave/matlab code I used to perform the comparison available, or if you would prefer I can just publish the graph itself on this blog, but before I do I would really like to see where your numbers come from and how it happens that they lie so perfectly on your curve. For example, in your table 1 you find that Mercury and the Moon both exactly have
— to four digits, presumably. This is all by itself simply not the case. Your estimate of Mercury’s temperature is egregiously low, and its albedo is not (according to most published work) equal to that of the Moon. Neither of them has a significant atmosphere, so one would expect their mean temperature to be determined by their actual albedo according to your own reasoning!
Yet somehow they end up having exactly the right surface temperature to have the same
in spite of that fact that physically, this is quite impossible by your own arguments. How did that work out, exactly?
rgb
I have also asked about the Galilean satellites, and have as yet received no reply to my question regarding the temperatures. Repeating Robert Browns point – where did the experimental data come from?
As a further complication, even calculating S0 for these satellites is problematic, unless allowance is made for a) tidal heating b) radiation from Jupiter itself and c) the time the satellites spend in Jupiter’s shadow – were any of these allowed for?
Robert Brown says:
February 19, 2012 at 10:18 pm
Yup. I have a similar problem with this aspect of the theory.
My thinking is that the formula shouldn’t work on planets with tenuous atmospheres for the very simple reason that the ideal gas law appears to break down under low pressures.
The clue is in the way that the temperature/height relationship, as defined by a stable adiabatic lapse rate, breaks down at the top of the troposphere (the tropopause) on every planet with a “mature” atmosphere. It happens on Venus, it happens on Earth, it happens on Titan, and it also appears (according to wiki) to happen on the gas giants – Jupiter, Saturn, Uranus and Neptune.
Even more significantly perhaps, it seems to happen at a similar atmospheric pressure (200mb-250mb) on ALL these planets.
I’d be very interested to hear the thoughts of all you professional physicists on this…….
B_Happy says:
February 20, 2012 at 12:15 am
I have also asked about the Galilean satellites, and have as yet received no reply to my question regarding the temperatures. Repeating Robert Browns point – where did the experimental data come from?
As a further complication, even calculating S0 for these satellites is problematic, unless allowance is made for a) tidal heating b) radiation from Jupiter itself and c) the time the satellites spend in Jupiter’s shadow – were any of these allowed for?
Good points B. However, those corrections seem as though they are in the wrong direction given that Io is very close to Jupiter, covered with a relatively dense atmosphere (that is still quite close to hard vacuum, of course), and yet cooler than Callisto which is so distant that tidal heating is surely ignorable. Then there is the conceptual difficulty of pretending that Europa — in an atmosphere that is the most tenuous of the four — has a surface temperature (given in the table as 73.4K but given on its Wikipedia page as 102K) that is completely unaffected by the fact that 2/3 of its insolation is reflected back to space without heating anything at all.
Just FYI, Wikipedia has the following data:
Moon T_s P_s
Callisto 134K 7.5pbar
Io 110K 300-3000 pbar
Ganymede 110K 2-25 pbar
Europa 102K 1 pbar
Given a common T_gb, this data alone completely confounds the “miracle” of equation 7. Io should be the warmest of the planets by far, and all of them should be much, much colder (commensurate with N&Z’s 73.4K for Europa) in order to fall close to their curve.
Wikipedia actually provides references for their numbers. Perhaps Nikolov and Zeller would be so good as to do the same? I’d like an idea of the uncertainties of those numbers as well — if the error bars are as large as they seem as though they really have to be (given the disparity between their numbers and the published/accepted numbers) then one can actually compute a p-value or chi-squared for their fit and see if it is reasonable.
rgb
[Reply] N&Z give full information on how they calculate the T_gb for airless bodies in their last paper. FYI Wikipedia has removed the reference to Mercury’s average surface temperature calculated from the ‘classic’ S-B method, since we pointed out that it was physically impossible for it to be higher than the simple average of the equatorial max and min empirical data.
Even more significantly perhaps, it seems to happen at a similar atmospheric pressure (200mb-250mb) on ALL these planets.
I’d be very interested to hear the thoughts of all you professional physicists on this…….
My own thoughts are that the usual greenhouse effect is determined by the height, and via the DALR temperature, at which the atmosphere becomes optically thin to radiation from greenhouse gases. It isn’t unreasonable that many gases would become optically thin at similar pressures. This also determines the tropopause — below the tropopause there is significant vertical convection from the differential heating at the surface and cooling at the top of the troposphere. So for the last four planets they attempt to fit — Mars through Venus — they all have a troposphere and a stratosphere and hence have a surface temperature that is related to a DALR, although I personally don’t find them lying on a single N_TE curve (Mars is well off) with N&Z’s T_gb. I haven’t tried computing N_TE with a physically plausible T_gb that uses the actual albedo of the planets involved, but I’m a bit doubtful that it will produce a particularly compelling fit. That’s on my agenda of future work to do with my little octave program.
[Reply] Both N&Z and Hans Jelbring agree Mars’ atmosphere is too thin to show a pressure effect on surface temperature. Using actual albedo rather than T_gb won’t work in N&Z”s equations. Willis didn’t understand this either.
The other Moons as you note have very tenuous atmospheres indeed — atmospheres that are already far thinner than the pressure at the tropopause on most planets — and IIRC only Triton has a troposphere at all, and it lacks a stratosphere. There isn’t any reason in the world to think that the physics that dominates their mean surface temperature in any way resembles the physics that dominates the surface temperature of Venus. For one thing even those Moons with greenhouse gases are optically thin and unsaturated and have very little greenhouse effect compared to a planet with an optically thick, saturated GHE.
And as I have noted and do not wish forgotten, N&Z’s equation 7 has completely unphysical reference pressures in it. How the reference pressure of 54,000 bar or 202 bar can arise in any sane way from the consideration of physical principles very much remains to be demonstrated. Personally, I reject it out of hand as evidence that the entire result is wrong unless and until most rigorously proven otherwise.
[Reply] I notice you still haven’t answered the question I last asked five days ago. I’ll be snipping any further repetition of your argument about ‘reference pressure’ since you are unwilling to engage in a discussion of its relevance or applicability.
Perhaps it is worthwhile to go ahead and show the results of applying N&Z’s own T_gb per planet to independently obtained estimates of planetary T_s to form N_TE.
http://www.phy.duke.edu/~rgb/loglong-nandz.jpg
It’s a log-log plot so that one can see the data (spread out over many orders of magnitude in pressure, otherwise). The leftmost x is the moon, then mercury, then the four circles are the Jovian moons, then the remaining x’s are triton, mars, earth, titan and venus. Note that I do not pretend that my numbers are certain, only that I can tell you where, and how, I got them, and that I think that they are pretty good ones unlikely to be more than maybe 10% off (less in the case of the Earth, Mars and Venus, which all have more or less permanent weather satellites and good data, more in the case of planets known only from single flybys and very long range Hubble studies — in many cases the error ranges I did find were easily 10% for the pressure alone (probably measured indirectly from pressure broadening of spectral lines, something with fairly large uncertainties given a signal from the entire atmosphere and not just the surface).
[Reply] Yes, please reference your data. Thanks.
The +’s are N&Z’s own data from Table 1 in their paper/poster. The curve absolutely precisely goes through the +’s — even a deviation of a few percent in either T_s or P_s would be enough to move them well off, as indeed occurs for all of the points but three in my refit.
How can this be? The + signs are presumably experimental data with uncertainties! There is a “miracle” here indeed!
rgb
[Reply] Did you use surface temperatures calculated with the stefan-boltzmann method N&Z have comprehensively shown to be wrong with empitical data for our Moon?
“Both N&Z and Hans Jelbring agree Mars’ atmosphere is too thin to show a pressure effect on surface temperature. Using actual albedo rather than T_gb won’t work in N&Z”s equations. Willis didn’t understand this either.”
Eh?????
If Mars’s atmosphere is too thin to show a pressure effect, then why is it in their training set, and why do N+Z quote it as a success? Are you claiming that their NTE values work, but actually have nothing to do with the pressure? And if the Martian atmosphere is too thin, why are Europa and Triton in there.
[Reply] Because although the atmosphere is too thin to warm the surface, their equations still work. “Are you claiming…” No, I’m not.
“Did you use surface temperatures calculated with the stefan-boltzmann method N&Z have comprehensively shown to be wrong with empirical data for our Moon?”
I would say they have asserted it to be wrong, not that they have shown it. Do you really think the temperature drops to 3K when the sun is not shining?
[Reply] The N&Z method assumes a zero heat capacity for the surface, but gets the average surface temperature right to within 6K for the Moon. The ‘classic S-B method’ gets the Moon’s average surface temperature wrong (too warm) by over 100K.
Tallbloke, did you miss Dr. Brown’s rather extensive comments regarding dimensional analysis and Fermi estimation in this thread? Or did they just go over your head?
[Reply] Robert has still not responded to my simple question, which is logically prior to his more rarified analysis. I notice you haven’t responded to the question I asked you when you interceded on his behalf either. Neither of you will be posting more of the same repetitive verbiage here until it they have been properly responded to. Ignoring pertinent questions and instead repeating your own claims is merely politician’s rhetoric technique which has no place in scientific discourse.
[Reply] Yes, please reference your data. Thanks.
But could we have a reference for N&Z’s data? Several people have asked for it. The success of the theory rests on their ability to match temperature and pressure data, but where does it come from?
[Reply] Thanks Nick, noted. I hope N&Z will address this in their next paper. Meanwhile, Robert has offered, and I have taken him up on his offer.
I said this elsewhere but I think it valid here:
Neither the Earth nor the Earth’s atmosphere are black bodies.To give black body status to Earth you have to take a point beyond the atmosphere as the ‘surface’ and only then apply SB.
Treating Earth and its atmosphere as two black bodies separated by a vacuum is wholly inappropriate because the Earth and its atmosphere are a single unit interacting primarily via non radiative processes which is where the Gas Laws come in.
So, for planetary bodies separated by a vacuum, apply SB but only at a point outside any atmospheres where radiative processes do indeed dominate exclusively.
For bodies not separated by a vacuum, such as a planet and its atmosphere, apply the Gas Laws because non radiative processes dominate.
AGW has applied radiative physics to a non radiative scenario and the outcome is garbage.
Applying the SB equations at the contact point between a planet and its atmosphere is no better than applying it at the junction between the Earth’s mantle and the crust.
The SB equations are only of relevance at the junction of atmosphere and space. They can never predict the temperature at the contact point between two differing materials within a planetary system.
Tallbloke, I think that you are really grasping at straws if you are trying to assert that the use of the complexxx unit “i” in mathematics or physics — or for that matter the use of general geometric division algebras of arbitrary grade, since complex numbers are just a step on an infinite series of geometries and number systems — has anything whatsoever to do with Fermi estimation and the appearance of a truly absurd reference pressure in a fit. [snip]
[Reply] I didn’t. I asked you to explain the physical basis for it. Can you do that?
Treating Earth and its atmosphere as two black bodies separated by a vacuum is wholly inappropriate because the Earth and its atmosphere are a single unit interacting primarily via non radiative processes which is where the Gas Laws come in.
I completely agree. But it is also completely off topic to the discussion at hand. Radiative balance only makes sense beyond the atmosphere, or if one wants to be very picky, one should really consider a sphere around e.g. the Earth at (say)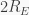
(well beyond the atmosphere) and compute the simple flux conservation equation:
(or in words, the integrated outgoing flux of the Poynting vector equals the rate of change of the total internal energy inside) averaged over a sufficient time and assuming that one can neglect work and stored energy, at least on average.
It isn’t even this simple — the notion of “average” has to be coarse-grained, we cannot really track the ultimate disposition of all of the retained energy when the one doesn’t balance the other — but in general this sort of equation describes the energy flux in and out of the Earth via radiation.
rgb
[Reply] The N&Z method assumes a zero heat capacity for the surface, but gets the average surface temperature right to within 6K for the Moon. The ‘classic S-B method’ gets the Moon’s average surface temperature wrong (too warm) by over 100K.
6K is over 2% error. Yet
to four digits in their table 1 data for both the Moon and for Mercury. Curious, don’t you think?
rgb
[Reply] I find it a good deal more curious that the climate science mainstream, and apprently, Duke physicists, still defend the classic S-B planetary equation when it has been demonstrated to be at odds with empirical data of planetary surfaces not be a couple of percent, but by over 50% (!?)
Tallbloke, I think that you are really grasping at straws if you are trying to assert that the use of the complexxx unit “i” in mathematics or physics — or for that matter the use of general geometric division algebras of arbitrary grade, since complex numbers are just a step on an infinite series of geometries and number systems — has anything whatsoever to do with Fermi estimation and the appearance of a truly absurd reference pressure in a fit. [snip]
[Reply] I didn’t. I asked you to explain the physical basis for it. Can you do that?
OK, I’m done.
Best of luck and all that.
rgb
[Reply] Robert has been defeated by an imaginary number. I never imagined that would happen. 🙂
It’s easy to see that N&Z could recast their equations to include a significating algebraic letter to represent their multiplication factor for their equation 7, just as engineers and electricians use ‘j’ in their equations for real world solutions that really work, even though they, and Robert are unable to explain the physical basis for it. Robert’s complaint about “absurd reference pressure” is therefore itself absurd. Of course, this only gets N&Z’s equation to the level of a heuristic, so this small victory doesn’t close the issue of the underlying physical basis. In the meantime, we’ll await N&Z’s log-log plot so we can compare it with Robert’s, and further ahead, more planetary data their heuristic can be tested against.
Ned Nikolov says:
The actual temperature profile in Earth’s atmosphere is more complex because of differential absorption of spectral solar radiation by air constituents with increasing altitude. The temperature raise in the stratosphere is due to an increased absorption of UV radiation by ozone (oxygen) molecules with height. Higher levels in the stratosphere absorbs MUCH more energetic UV light than lower levels. The pressure effect in terms of relative thermal enhancement is still there and pressure falls with height, but the UV absorption by the higher levels is so much more than that at lower levels that the lapse rate becomes actually inverted. This is similar to the situation we have with Earth and Titan. The NTE factor for Titan is larger than that for Earth (due to higher pressure on Titan), but Titan’s surface is much colder than Earth because it receives/absorbs much less solar radiation … The temperature increase with height in the stratosphere has NOTHING to do with the proposed effect of GH gases to slowdown or reduce infrared cooling to space. There is no such reduction of cooling! Instead, there is an increased absorption of UV radiation with height.
Reported temperatures of up to 2,500C in the thermosphere reflect a bit of a confusion, because these are temperatures (energy states) of INDIVIDUAL molecules, not for the gas as a whole. For comparison, the temperatures typically measured and reported in the troposphere refer to the energy state of the entire gas volume. The latter are palatable temperatures as opposed to individual-molecule temperatures. Due to an extremely low air density in the thermosphere, the palatable temperature there is quite low! In other words, if you stick a normal thermometer into the thermosphere, it will measure temperatures that is WAY lower than 2,500C … see this Wikipedia page:
http://en.wikipedia.org/wiki/Thermosphere
Palatable temperatures are basically not compatible with temperatures reflecting the energy state of individual molecules. So, comparing thermospheric temperatures with tropospheric temperatures is a bit like comparing apples and oranges … Not many people realize that fact!
– Ned
Ned makes a good point about the difficulty of comparing temperatures at different levels.
That is what makes it virtually impossible to demonstrate with our current knowledge and sensing systems that the energy flow from ground to space for a given planet with an atmosphere does actually match the rate of flow that results from the dry adiabatic lapse rate.
Logic, however, suggests that it must be so if the atmosphere is to be retained at all or kept in gaseous form for billions of years.
I agree completely that from tropopause upward there are different thermal responses to solar irradiation at different levels. Indeed that is what alters the vertical temperature profile from above so as to affect the air circulation patterns below the tropopause whilst, at the same time, changes in sea surface temperatures are trying to achieve the same effect from the bottom up.
Climate change is primarily a consequence of the ever changing balance between the top down solar and bottom up oceanic influences on the rate of energy flow through the system in place of any change in the energy content of the system.
Tallbloke, I find it curious that people who disagree with you are required to answer your seemingly arbitrary questions under penalty of snip. Curious.
To answer your question to me; 2i would be another number that, when multiplied by itself, would result in negative number. I suspect that you won’t find that answer satisfactory. I’m not really sure what you’re getting at, though. I wasn’t even certain that your question was serious.
And to be clear, I wasn’t trying to “intercede” on Dr. Brown’s behalf. I was hoping that you would reconsider your question and perhaps find a better way to express it. As stated, your question to him does not make sense. Mathematics is abstract and none of it has any physical meaning unless it is being applied to a physical system. Since you did not provide any context (e.g. a particular physics formula), of course ‘i’ has no physical meaning. How could it?
[Reply] When I find time, I’ll make a post out of it so it can be presented more completely, and discussed more thoroughly. Robert misrepresented what I was asking for, and used that misrepresentation as the platform for (yet another) lengthy rant about N&Z. Nearly all of it was repeating earlier comments he made. I had already stated (twice) my intention to curtail further rants which didn’t address my question. Robert chose to answer a different question of his own invention and then rant. That’s why I snipped it early and put him straight about what I was asking for.
Joel Shore says:
Robert Brown is someone who you ought to have been able to keep on your side if you were at all reasonable given that he seems strongly pre-disposed toward a skeptical position on AGW. Unfortunately for you, however, he also knows enough physics not to believe silly pseudoscientific nonsense like you and Nikolov and Zeller are peddling.
By the way, you really seem to have no real clue about the science that you are attacking, which means you spend most of your time attacking strawmen.
[Reply] Hi Joel, You set ’em up, I knock ’em down. 😉
So is that your considered opinion on the vertical temperature profile of the troposphere? That N&Z’s idea that the main cause of it is the Sun’s energy interacting with the gradient in air pressure caused by gravity, and the consequent higher near surface density with its higher heat capacity is: “silly pseudoscientific nonsense”? it’s very noticeable that you won’t confirm or deny this basic point. I think you are being evasive and unresponsive. Neither of these traits are conducive to proper scientific discourse, so answer the question please.
For myself, I think the ocean has a lot to do with the reason surface T (and consequently marine surface air temp) is what it is. This is because the Sun heats it faster with shortwave radiation which penetrates it than it can cool overnight by evaporation, convection, conduction and long wave radiation (which has a tough time escaping). That is, until it gets up to a temperature where those processes removing heat from it (and all of them do on the average) can work at a rate which sets a rough equilibrium. That temperature seems to be around 275K judging by the bulk of the ocean. This also depends on near surface air temperature to a small extent ( but only small, since on average the ocean is warmer than the air, and ‘back radiation’ can’t penetrate the surface anyway) but I think N&Z are right in the wider sense that if the mass of the atmosphere wasn’t exerting pressure on it, the ocean would have boiled off into space.
So I’ll continue to provide a venue where the details and premises of their theory, and its strengths and weaknesses, can be calmly discussed without being trash talked by you and Willis, and gish-galloped into the ground like you and he and Robert did at WUWT. As for the quality of Robert’s science, the news that the laws of thermodynamics have been considered and defined in terms of energy rather than heat since the 1880’s doesn’t seem to have reach Duke yet. He is knowledgeable in some specialist areas, but at the end of the day he’s just another person with a false sense of infallibility and a propensity to talk (much) more than listen. He should himself have paid more attention to the Feynman lecture he berated N&Z with IMO.
I don’t see much in the way of Feynmannian humility in Robert, or you, or Willis for that matter. All of you need to read the Loschmidt thread.
“[Reply] I find it a good deal more curious that the climate science mainstream, and apprently, Duke physicists, still defend the classic S-B planetary equation when it has been demonstrated to be at odds with empirical data of planetary surfaces not be a couple of percent, but by over 50% (!?)”
I double agree Roger. I am shocked too at the general attitudes of men of science that should be inquisitive. No wonder sceince is in the shape it is in. I never heard Ned or Karl claim that those four best-determined parameters were set in stone. There is one point where I do agree with Dr. Brown, at some point in the future the physical process needs to be found, explained, and those parameters take on proper form in the units. Heck, the entire equation may even end up in a different form for what anyone knows at this point, but that curve stays. It is too consistent, well formed, and smooth to not drive the future investigations to find out why it exists.
“empirical data of planetary surfaces not by a couple of percent, but by over 50% (!?)”
Well, you would get that if you define the SB ‘surface’ as being within the system beneath an atmosphere and then fail to apply the Gas Laws.
Might as well apply it between the crust and the mantle !!!
[Tallbloke reply to rgbatduke]
“Robert has been defeated by an imaginary number. I never imagined that would happen. 🙂 “
Nor me! Being a physicist he should be used to dealing with the imaginary stuff which has been invented to protect the ‘standard model’ and has lead us to today’s brand of unphysical physics.
No wonder climate science can’t understand what is actually going on when the underpinnings are collapsing. Time to go back to a mechanical explanations for what we see.
About the impact of rotation on airless planet. I did numerical calculations for the entire equator for two cases a. nonrotating b. infinite rotating
a. Tmean(GB) = 0,5 Te
b. Tmean(GB)= Te
Conclusion temperatures are converging with rotation as postulated by A.Smith(2008)
When I looked to the results it made sense to me, half of the surface is not used in case a.
I made a brief post with calculated temperatures and a brief explanation and mailed it to WUWT.
If there is interest in an extensive post with more details I will submit.
Willis Eschenbach says:
April 26, 2012 at 2:21 am
Lucy, you never did understand the problems I exposed in Nikolov and Zeller’s work at “The Mystery of Equation 8“. In fact, in that thread you said:
I get the feeling that there are a number who can see Willis’ limitations who are no longer coming here to post.
… to which another poster replied about why some people, including Nikolov and Zeller, were no longer posting on that thread
Yes, their goose has been well and truly cooked by Willis’s article, their fox has been shot. Anyone with a basic knowledge of science, or in this case,just basic mathematics, is aware that when the number of ‘fudge factors’ exceeds the number of unknowns then any ridiculous proposition can be formalised. It isn’t really a ‘Miracle’. Well done Willis – that’s what I call a game-changer.
Lucy, have you ever thought that you and Tallbloke do harm to the sceptic cause by promoting nonsense?
Indeed, the poster was right, you do harm …
I note you haven’t attempted to reply at WUWT to their rebuttal here of your serial maths errors in your vicious and vacuous attack piece:
In that post, you also spoke highly of Hans Jelbring and his cockamamie hypothesis that you can get ongoing energy from gravity, a hypothesis that I discussed in Perpetuum Mobile, and that Dr. Robert Brown totally blew out of the water with a formal proof in Refutation of Stable Thermal Equilibrium Lapse Rates. Jelbrings hypothesis was obviously and glaringly wrong. But you, you thought Jelbring’s hypothesis was good, solid science.
It rests on which side of the debate over the as yet after 120 year unresolved Loschmidt paradox. I doubt you have the finesse to understand such nuanced issues in the history of science.
Heck, even Nikolov and Zeller wouldn’t answer my questions. They refused to reply, to defend their work, or to even discuss their work, they ran like vampires at sunrise from the huge problems I pointed out in their work … and now you want me to listen to you explain their brilliant science? Really?
They didn’t get the right of reply at WUWT, so they demolished your disgusting ad hominem attacks and appalling maths errors on this thread instead.
Likewise, Lucy has responded here: https://tallbloke.wordpress.com/2012/04/24/the-connection-to-evolution-is-a-culmination-of-this-work-dtu-director-on-svensmarks-new-paper/#comment-24093
You, Willis, are a disgrace to the principle of fairly and courteously conducted scientific debate.
Tallbloke,
I wonder if you agree with the proposal that maximum radiative transfer of energy between non contiguous bodies occurs in a vacuum. If you agree with this, it should take you about ten seconds to realise that Interposing anything at all – CO2, pixie dust, whatever, cannot possibly result in anything other than a drop in received energy, and hence a drop in temperature in an already cooling body such as the Earth.
Anyone who calculates the Earth to be warmer than it is, is a fool. The Earth probably (nobody was there at the time) had a surface temperature in excess of 5000K at the time of its creation. The surface has demonstrably cooled to the present time. Has it stopped cooling yet? Highly unlikely, given that most of he Earth by mass is still molten.
Sitting in a vacuum, receiving insufficient insolation to hold the temperature any higher than it is now, the Earth should continue to cool.
So, a rise in the Earth’s store of energy may be caused temporarily by the mechanism which results in the creation of CO2 – oxidation of carbon. This is radiated away.
I note that many people seem to be enthralled by analogies – so here’s one.
Heat a more or less spherical chunk of steel up to white heat. Don’t record the initial temperature.
Wait until it has cooled a fair bit. Don’t record the length of time it has been cooling. Now calculate the temperature using SB or any other equation you like. Measure the actual temperature. Explain the difference between the calculated and “real” temperature using words like “back radiation”, “forcings”, “sensitivity”. “radiative transfer”, or any buzz words that mean whatever you want them to mean.
I think I am right. I will change my views if I am wrong. Nobody seems to be able to discuss my initial understanding about radiative transfer of energy.
Thanks,
Mike Flynn.
Hi Mike, and welcome.
“Interposing anything at all – CO2, pixie dust, whatever, cannot possibly result in anything other than a drop in received energy,”
Co2 is largely transparent to incoming wavelengths from the Sun, but absorbs at some of the longer outgoing wavelengths. The cloud albedo is a much bigger blocker of incoming sunlight than the absorption direct into the atmosphere.
“Sitting in a vacuum, receiving insufficient insolation to hold the temperature any higher than it is now, the Earth should continue to cool.”
So far as I can tell, it receives just enough radiation to hold a steady surface temperature. It is thought that only around 0.1W/m^2 is escaping from under the crust on land. I suspect it loses a bit more than that into the ocean though.
Tallbloke,
Thank you for your response. What I want to know is whether there is any known material in the universe which allows transmission of EMR better than a vacuum. I gather from your answer there is not, but you haven’t specifically answered me.
As far as I am aware, there is no such thing as a one way insulator. In any case, it matters not whether the wavelengths are long, short, or in between. If a body absorbs energy of any wavelength, its energy content will increase, with the inevitable consequences. In he case of CO2 etc, the energy absorbed raises the temperature of the CO2, which, then radiates the increased energy away. I believe this is why NASA is able take IR photos of CO2 distributions within the atmosphere, amongst other things.
So, I wonder if you agree about the vacuum thing? Regardless of re-radiating, reflecting, refracting, or otherwise attempting to create something from nothing, we can’t seem to achieve Earth surface temperatures anything like those on the Moon. The main difference to me seems to be the atmosphere reducing the efficiency of insolation.
I should perhaps also point out (and I mean no offence), that people talking about radiation from the Earth’s surface forget that when energy radiates away from the Earth’s surface, the temperature of the surface drops by precisely as much as it rose after absorbing the same amount of energy.
So any re-radiation, “back radiation”, or whatever you want to call it, can never replace that temperature drop in reality. Of course, a perfect insulator would ensure that the body’s temperature would remain the same, but such things do not exist.
Anyway, the whole thing is certainly fascinating. If I am correct, and about the only man made warming is the warming created by Man in the process of oxidising carbon in the main to create CO2, (I know there are a whole lot of other methods of heat generation) then worrying about “climate change” in the sense that we can affect the outcome by reducing GHGs is the waste of a good worry!
Sorry to be so long winded, but I sometimes (usually) find difficulty in getting a definite answer to a simple question. I didn’t finish high school, and I find a lot of the information on the Internet contradictory.
Thanks for your kind help.
Mike Flynn
Hi Mike: I agree a vacuum transmits EMR best.
Co2 radiates in all directions, not just ‘away’ in the sense of ‘to space’.
“we can’t seem to achieve Earth surface temperatures anything like those on the Moon. The main difference to me seems to be the atmosphere reducing the efficiency of insolation.”
Neither as hot, nor as cold at the extremes. The atmosphere and coupled ocean spreads heat, creating a higher average temperature than the Moon’s (due to Holder’s inequality) even though clouds make our albedo three times higher than the Moon’s – reflecting more of the incoming solar radiation directly back to space, ” reducing the efficiency of insolation.” as you note. Additionally, atmospheric mass enhances surface temperature by other mechanisms due to surface pressure.
‘Back radiation’ is a minor bit player in our estimate, so we agree about that, although we agree for different reasons. There is back radiation, and it is absorbed by the surface, but as you point out, the surface is cooled by evaporating, emitting radiation and convecting, before the back radiation returns, and 7/10ths of the surface (the ocean) absorbs all the back radiation in the first few nm, where it mostly promotes ocean surface cooling evaporation.
So the surface temperature is raised by something else. N&Z say it’s pressure enhancing the lower atmospheric temperature. I say it may be partly that, plus the limit surface pressure places on the rate of evaporation from the ocean surface.
Cheers
TB
“plus the limit surface pressure places on the rate of evaporation from the ocean surface.”
Actually the energy cost of a given amount of evaporation. Not the rate.
The rate is governed by lots of other factors.
Pressure governs the value of the latent heat of evaporation.
At 1 bar it is currently around 5 units of energy taken up by the phase change for every 1 unit of energy input.
Reduce pressure and it will be more than 5 to 1.
Increase pressure and it will be less than 5 to 1
(Hope I’ve got that the right way round – in a hurry at the moment)
Those relationships set the system equilibrium temperature for our water planet. The atmosphere just follows on.
Hi Tallbloke,
I notice that, in general, it seems to be taken as gospel that the Earth is somehow “warmer” than it should be, and that this needs an explanation. Terms such as “indisputable”, “irrefutable”, “well proven” and the like abound in supposedly serious discussions.
The physical observations seem to indicate otherwise. The solidified crust of the Earth (on which we live), would represent about a millimeter or so, on a globe of molten rock some 200 mm in diameter (assuming my mental arithmetic and memory are reasonable.)
This combination of molten and solid(ish) material we call the Earth, is cooling. You imply that the rate is not significant, at an average of 0.1 W/m^2. It is worth considering that if incoming energy is to rise by that amount, the Earth would cease to cool, and would melt the crust in due time, as the temperature gradient between the core and the surface became zero (apart from effects due to turbulent flow within the liquid blob.) So whatever the total loss of energy is, I would prefer it to be as higher rather than lower. I have no wish to fry due to a minor rise in the Sun’s output.
In any case, as you rightly state, the Earth’s surface loses energy at some rate not easily quantifiable. This results in less energy within the Earth, and a subsequent fall in temperature. This loss is not made up by insolation, as the best that the Sun can do is to warm small portions of the surface, or things on the surface, to no more than about 90C. As you agree, the amount of insolation reaching the Earth’s surface per unit unit area is less than that of the Moon. If the average Earth surface temperature is higher, might not the fact that the Earth is >99% molten, and losing heat through the crust, thereby raising the crustal temperature well above what the Sun can account for, be the cause?
N&Z say it’s pressure enhancing the lower atmospheric pressure, and they may be right. An actual experiment or two would help. At the moment, I am happy with the molten earth slowly cooling. I’m not sure whether it is at all relevant, but pressure doesn’t seem to warm the abyssal depths much.
Maybe it only applies to gases, and this should be easy enough to demonstrate.
Finally, may I point out that the Moon’s interior appears to be considerably colder than the Earth’s. Once again, it seems logical that the difference in surface temperatures is depressed rather than raised by the presence of an atmosphere. Any observed surface temperature differential between the Earth and the Moon, is purely due to the fact that the Earth has a hotter interior closer to the surface.
Live well and prosper.
Mike Flynn.
PS Sorry to be a pain, but I think people who believe the atmosphere somehow “warms” the Earth suffer from collective infectious delusionalism. The luminiferous ether, phlogiston, phrenology, gastric ulcer causation, circular planetary orbits – take your pick. All a part of the same continuum. Pity about the wasted money, but I suppose we need more poverty and starvation. We certainly try hard enough.
[…] Nikolov & Zeller: Reply to Eschenbach […]
Very entertaining. Even with no radiation, internal, incoming or outgoing,
temperature is lower higher up. In order to enhance surface temperature,
does any internal radiation have to be present? (Helium only atmosphere,
with no trace gases)
I am thinking that (within limits of properties) condensates self adjust,
to Maximize Cooling, minimize warming?