Many other people have noticed Phi relationships in the solar system in the past, from Kepler onwards, and there are several websites which cover this interesting topic. But up until now, so far as I know, no-one has been able to find a single simple scheme linking all the planets and the Sun into a harmonious whole system described by the basic Fibonacci series. A couple of weeks ago while I was on holiday, I had a few long ‘brainstorming sessions’ with Tim Cullen, and decided to roll my sleeves up and get the calculator hot to test my ideas. What I discovered is laid out below in the style of a simple ‘paper’. Encouraged by an opinion from a PhD astrophysicist that this is “a remarkable discovery”, I will be rewriting this for submission to a journal with the more speculative elements removed and some extra number theory added to give it a sporting chance of acceptance. For now, this post establishes the basics, but there is much more I have discovered, and I will be using some of that extra material in more posts soon.
Relations between the Fibonacci Series and Solar System Orbits
Roger Tattersall – February 13 2013
Abstract
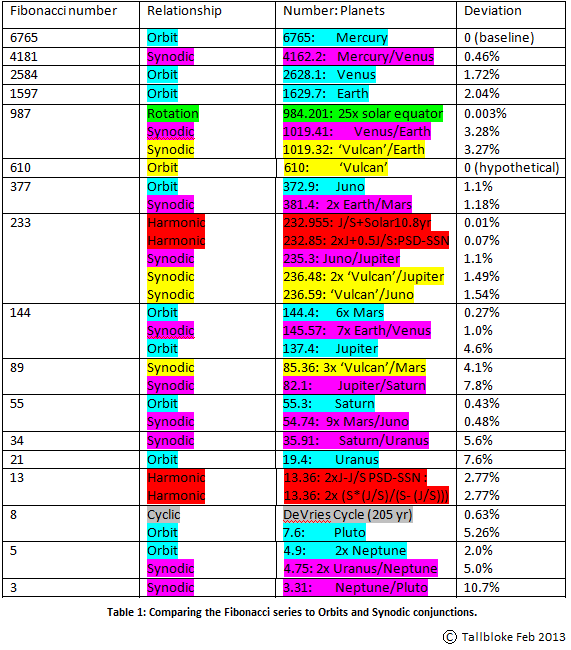
The linear recurrence equation: an = an-1 + an-2 with the starting conditions: a1 = a2 = 1 generates the familiar Fibonacci series: 1,1,2,3,5,8,13… This paper will use the first twenty terms of the sequence to demonstrate a close match between the Fibonacci series and the dynamic relationships between all the planets, and two dwarf planets in the Solar System. The average error across the twenty eight data points is demonstrated to be under 2.75%. The scientific implication of the result is discussed.
Introduction
Since it was noticed that five synodic conjunctions occur as Earth orbits the Sun eight times while Venus orbits thirteen times, many attempts have been made to connect the Fibonacci series and it’s convergent ‘golden ratio’ of 1.618:1 to the structure of the solar system. Most of these attempts have concentrated on the radial distances or semi-major axes of the planet’s orbits, in the style of Bode’s Law, and have foundered in the inner solar system.
The present paper adopts a different approach, in order to simultaneously study the dynamic relations between planet pairs as signified by the frequencies of their synodic conjunctions in addition to their individual orbits. A static analysis of semi-major axes is inadequate to an understanding of a dynamic solar system in the same way that statically balancing a flywheel cannot reveal the out of balance forces which will cause vibration when it is rotated at high speed.
Method
The highest number in the series used (6765) is allowed to stand for the number of orbits of the Sun made by Mercury, the innermost planet. The number of orbits made by the other planets and dwarf planets during the same time period of ~1630 years taken by Mercury to complete 6765 orbits are calculated. Additionally, the number of synodic conjunctions between adjacent planet pairs made in the same period is calculated using the method derived by Nicolaus Copernicus:
Period = 1/((1/faster orbit)-(1/slower orbit))
Additionally, the harmonic periods associated with the Power Spectral Density (PSD) study made of the sunspot number by talkshop contributor ‘Bart’ and used in the subsequent posting on Jupiter and Saturn’s relationship with the solar cycle and independently confirmed by Scafetta 2012a[7] are included. The results are then compared to the descending values of the Fibonacci series and the deviations from the series calculated.
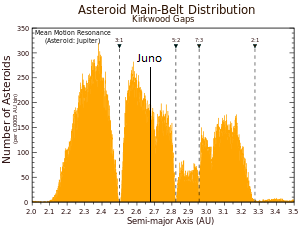
Juno is selected as representative of the Asteroid Belt as it lies near the middle of the main core at a distance of 2.67 AU. By Kepler’s third law this object has an orbital period of: P=(SQR)2.673=4.36yr.
Results
Results are tabulated in table 1. The hypothetically vanished planet ‘Vulcan’ is shown in order to demonstrate the interesting phi relationships which would have existed given its 2.67 year orbit.
Discussion
This is a startling result. There is no currently accepted physical mechanism which can explain the clear and strong link between the Fibonacci sequence, the dynamic motion of the solar system, terrestrial cyclic phenomena at around 60 years and 205 years and solar activity levels. The underlying ratio is Phi, known as the golden section or ratio. This ratio does manifest itself elsewhere in nature. In plant biology, Phi is well known to appear in the spacing of leaf stems and the packing of seed heads. The leaf stem spacing maximises sunlight exposure and the seed packing maximises abundance[1]. In Geology, Phi relationships are evident in atomic, quasi-crystalline and other chemical structures[2].
Space has no crystalline structure. However it does have gravitational fields and electromagnetic fields permeating it. What kind of interaction of these fields with matter could bring about a situation whereby, approximately 4.5 billion years after the formation of the solar system, such close relationships to Phi are found to link every planet and two dwarf planets in the solar system? Evidently, harmonic and other periodic perturbations between planets and planet pairs have helped shape the system, and continue to maintain its internal relationships.
The average deviation from the Fibonacci series for the eight planets plus two dwarf planets orbits is 2.75%. This compares well with Bode’s Law which exhibits a 15% average deviation. Solar activity cycles are represented by the inclusion of results from a Power Spectral Density (PSD) analysis which finds sunspot (SSN) activity peaks at 19.86 and 23.72 years, generating harmonics at 10.8 and 122 years[3]. This suggests that there is a link between planetary motion and solar activity levels.
Because the Sun’s gravity diminishes on an inverse square law, perturbation between Jovian planets will affect their orbits more strongly than the inner planets. Consequently, the Jovian planets excepting Saturn show a bigger deviation from the Fibonacci series than the three innermost planets.
It is suggested by Miles Mathis that inside Newton’s gravitational equation: F=GM1M2/r2 and Coulomb’s similar charge equation: F = kq1q2/r2 there is a unified field rather than two separate forces described by the two equations[4]. Mathis demonstrates that with a minimum of postulates, a fully mechanical ‘pool ball physics’ can be developed. As well as providing a gravitational acceleration bringing extended bodies together, it also contains a repulsive electromagnetic force which although weak in our everyday experience, can become significant at the scale of astronomical bodies when they are in proximity. Importantly, the gravitational acceleration and the repulsive force scale differently as distance changes due to the different properties of the bodies they relate to.
This may explain why empty viable orbits are free of formation debris; the changing of the planetary orbits to create the most efficient order has over time traversed and swept the solar system clear of debris. The exception is the Asteroid Belt between Mars and Jupiter. Some evidence suggests its formation may be recent (3.2Ma).
Additionally, Mathis’ ‘foundational E/M field’ pervades space at varying densities (dependent on the proximity of emitting bodies), providing a ‘background’ against which the ratios of forces exerted by bodies will operate. Mathis suggests that rather than trying to understand Phi in isolation, we can only appreciate the way that the two quantities which form the ratio can operate mechanically, by understanding the way in which they are relative to the ambient field in which they operate[5]. This is not a proposal for a ‘Universal Aether’, but for an interplanetary space which contains a density varying field of charge and spin bearing photons being constantly emitted and absorbed by matter. In a solar system with over 98% of the mass at the centre in a strongly magnetic star, and planets exhibiting Phi relationships in their orbital and synodic periods, this implies a relationship between Phi and the inverse square laws governing gravity and electro-magnetism.
UPDATE 27-8-2013 Since writing this paper, Miles Mathis has demonstrated that Phi contains the inverse square within itself .[8] Consider boxes 2 and 3 in the Fibonacci spiral construction (Right). “The radius of the second box is r = 1/φ. The radius of the third box is r = 1/φ2. I would call that an inverse square relationship. If we then compare box four directly to box three, we get the same relationship, and so on. If we look at each box as a field component (or fractal) instead of as part of a series, we do have an inverse square fall-off. We know that box 4 is to 3 as 3 is to 2, so if there is an square relationship between 3 and 2, there is a square relationship between them all. The reason we don’t find that inverse square relationship between box 1 and 2 is that box 1 is arbitrarily assigned the number 1. But our series is not based on the number 1, it is based on the number 0.618. That is why box 2 is our foundation, not box 1. This is also why we don’t find a square relationship between box 4 and 3, with the given numbers. The given numbers are written as functions of 1, not of .618. In other words, if we divide 1/φ2 by 1/φ3 , we don’t find a square. But again, that is because the series is not afunction of 1/φ2 . It is a function of 1/φ. So the only relationship that will directly tell us that the series IS based on the square law is the relationship between 3 and 2, as I showed.”
Conclusion
The logical conclusion is that feedback is present via perturbations between the planets and Sun which arranges the planets into an order which minimises work done, enhances stability and maximises entropy. This calls to mind the constructal law, stated by Bejan in 1996 as follows: “For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it.”[6]
A true system contains cybernetic feedback. The Phi relationships demonstrated here are evidence that the solar system truly is a system in the full sense of the word.
References
[3] https://tallbloke.wordpress.com/2011/07/31/bart-modeling-the-historical-sunspot-record-from-planetary-periods/
[6] Bejan, Adrian (1997). “Advanced Engineering Thermodynamics,” (2nd ed.). New York: Wiley.
http://en.wikipedia.org/wiki/Constructal_theory
[7] Scafetta, Nicola (2012a) “Multi-scale harmonic model for solar and climate cyclical variation
throughout the Holocene based on Jupiter–Saturn tidal frequencies plus the
11-year solar dynamo cycle” JASTP
Tallbloke's Talkshop 
@wayne: the Chap8 file mentions The observational basis for JPL’s DE 200, the planetary ephemerides of the Astronomical Almanac, wish we had at least this level of detail, reference and (mathematical) accuracy for geocentric climate data …
“I’m satisfied that there are real relationships here. It’s not random, and Roger A’s precision argument can’t show that it is anyway, for the reasons given above.”
TB, you’re misreading me. I agree there are real relationships here and that they’re not random. In fact I’ve already presented a number of examples that strike me as very real and non-random, in particular the log plot of the orbital distances of the Galilean moons of Jupiter, which has a trend very close to Phi.
I also agree that my “precision argument” doesn’t prove these relationships don’t exist. It was never my intention to prove they don’t exist. I’m simply pointing out the difficulty of expressing them in terms of whole numbers, which don’t seem to occur very often in the solar system.
@ RA
The synodic relationships offer another route to finding the Phi links, e.g.:
89 Jupiter-Saturn = 1618 Jupiter-Earth
9 J-S = 89 Saturn-Mars
233 J-S = 34 x 3 Saturn-Uranus
etc.
89 J-S may also be the nearest we get to a whole number match (60 S and 149 J) – 2.5 days difference in 1767+ years. Probably not a coincidence that these are the two biggest planets and of course neighbours.
Roger A: OK, that’s good to hear. I think the value of ‘doing the checks by hand’ is in discovering the interesting coincidences pop up. Like the near whole number of rotations involving V & E that was the same number as the orbits in a subdivision of the synodic precession cycle. It’s those sorts of observations which have enabled Stuart and I to make some sense out of all this. Still some way to go before we can generalise ‘rules’ though…
Rational Numbers Distribution is linked to resonance phenomena and also to stability of oscillating systems
Note this author arrives at phi (his number M1) and (quote) takes Laplace’s classic works forward (unquote). Ah, he puts number distribution at work for orbital radii of planets and also orbital periods.
oldbrew you made a remarkable work, especially your calculation using conjunction Jupiter-Saturn, I can assure you this is not only conjecture you touch it with a niddle especially this part :
“25560.276 / 178.74 = 143.00255 (no. of Jose cycles in sopc)
25560.276 / (143 x 16) = 11.1715 (one solar cycle, 16 per Jose cycle)
25560.276 / 19.86 = 1287.02 = 143 x 9
9.93 x 365.25 = 3626.9325 days
3626.9325 / 25.38 = 142.9 (no. of solar rotations in 9.93 years)
NB 9.93 x 9 = 89 (89.37)
(143 cf. Fibonacci 144 ?)
24007.816 / 168 = 142.904 (143) ”
Thank you TB to open this new door here, with new opportunities. I look forward to read more about your discoveries of this subject oldbrew.
@ Chaeremon
Not sure what to make of that paper, but as you say the author does include phi in his workings.
@ Greysen
Thanks for your interest. You can read some newer posts on this topic by putting ‘Phi’ in the ‘search this site’ box at the top left of the page.
From the recent exchanges it looks increasingly like we are witnessing an edge of chaos/self-organised criticality phenomenon here where the solar system dynamical symmetries are poised in a phase-transition/cantor set zone that allows for universal computation as it fine tunes optimal period, spin/angular-momentum rates, gravitational/EM resonance-minimisation and the like in the face of the resistances it encounters as it coils around our undulating galactic disk (whose spiral arms are BZ-like reaction waves of auto-catalytic star-formation).
As Adrian Bejan said to us in London this May 2013 when we visited ARUP’s Foresight & Innovation team, just look for what is flowing in the system as it seeks optimal freedom to flow and to morph and you will solve your problem.
The optimal, analogical geometric signatures of these Constructal law processes over time will reveal nested φ relationships because this is an innate, fundamental systems evolution constant of nature, a geometric manifestation of the principle of least action. http://asynsis.wordpress.com/2011/05/26/dynamical-symmetries-asynsis/
@ Chaeremon, in Dombrowski’s article, thanks for the interesting read, that is a strange sequence he is using indeed! You can find in that integer set that, for one thing, each is the continued fraction of that single integer repeated. Neat. But the more surprising fact is that every odd integer as the power of the silver ratio can be found as the fraction portion plus the integer entry itself. For example:
1 is 1 + Φ^1
4 is 4 + Φ^3
11 is 11 + Φ^5
29 is 29 + Φ^7
76 is 76 + Φ^9
199 is 199 + Φ^11
and so on. Quite close on the periods. At first I thought it was popping out the primes for I misread the 9th root entry at 76 but it ended up being just all odd powers. I’ll say again, that’s one curious sequence.
Hmm… and running backward into the negative integers it is just Φ^p, p being all odds. But the bases grow very rapidly, nearly exponential or maybe a form of a polynomial?
-1 is Φ^1
-4 is Φ^3
-11 is Φ^5
-29 is Φ^7
-76 is Φ^9
-199 is Φ^11
‘Place your mouse over this image, and you will see the Fibonacci spiral at work!’ – it says here:
http://www.fabulousfibonacci.com/portal/index.php?option=com_content&view=article&id=4&Itemid=12
3 Uranus-Earth conjunctions = 2 x Phi Neptune-Earth conjunctions
because (using NASA data):
63 U-E @ 396.66d = 24989.58 days
68 N-E @ 367.49d = 24989.32 days
63 = 21 x 3 and 68 = 34 x 2
so
21 x 3 U-E = 34 x 2 N-E
divide both sides of the equation by 21
3 U-E = 34/21 x 2 N-E
34/21 is Phi
so
3 x U-E = 2 x Phi x N-E